christianb93

The protected mode in the x86 architecture

Modern operating systems would not be possible without the ability of a CPU to execute code at different privilege levels. This feature became available for mainstream PCs in the early eighties, when Intel introduced its 80286 and 80386 CPUs, and was readily employed by operating systems like Windows 3.11 and, of course, Linux, which Linus Torvalds once called “a project to teach me about the 386”.

When an 80286 or 80386 CPU (and all later models) is starting up, it is initially operating in what is called real mode, and behaves like the earlier 8086 which is the CPU used by the famous IBM PC XT. To enjoy the benefits of protected mode, the operating system has to initialize a few system tables and can then switch to protected mode. It is also possible, though a bit harder, to switch back to real mode – and some operating systems actually do this in order to utilize functions of the legacy BIOS which is designed to be called from real mode.

One of the features that the protected mode offers is virtual memory and paging, a technology that we have already discussed in a previous post. In addition, and maybe even more important, the protected mode allows code to be execute in one of four privilege levels that are traditionally called rings.

Privilege levels

At any point in time, the CPU executes code at one of four ring (ring 0 to ring 3). The current ring determines which instructions are allowed and which instructions are forbidden, with ring 0 – sometimes called kernel mode or supervisor mode – being the most privileged level, and ring 3 – typically called user mode – being the lowest privilege level.

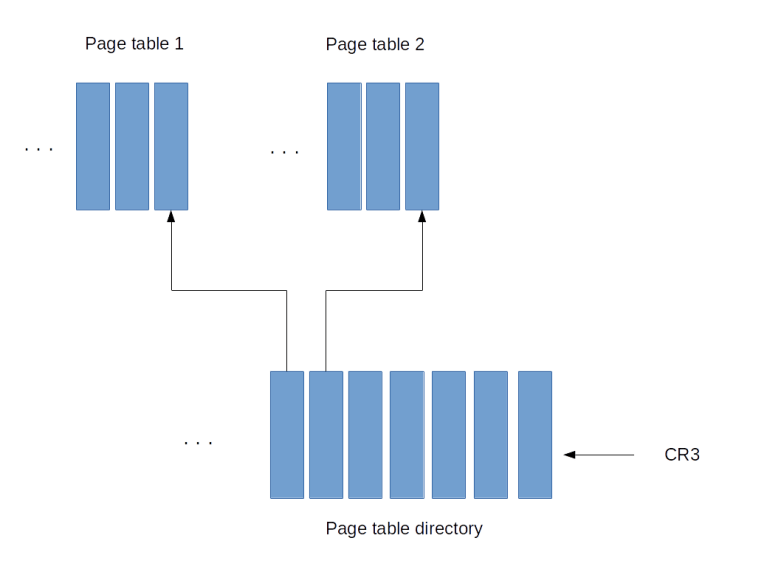
Some instructions can only be executed in ring 0. Examples are the instructions STI and CLI that start and stop interrupt processing (and potentially bring everything to a grinded halt as modern operating systems are interrupt driven, as we have seen in a previous post) or the command to reload the register CR3 which contains the base address of a page table directory and therefore the ability to load a new set of page tables. It is also possible to restrict the access to hardware using I/O ports to certain rings, so that code executing in user mode can, for instance, not directly access the hard drive or other devices.

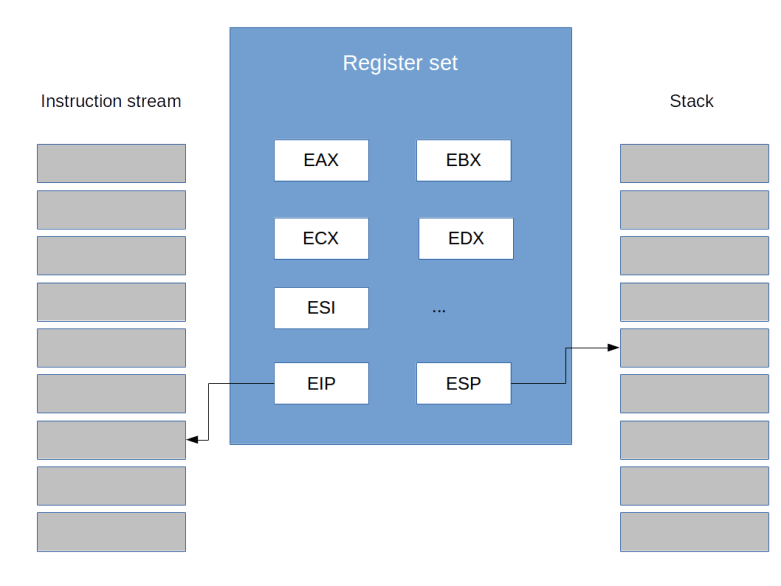
Technically, the current ring is determined by the content of a special register called the code segment register (CS) – most likely an old friend of yours if you have ever written assembly code for the 8086, we get back to this point further below. As so often in the x86 architecture, this is an indirect mechanism. The CS contains a pointer into a table called the global descriptor table (GDT) which again holds the actual descriptions of the segments. Part of each entry is a two-bit field which specifies the ring. Thus if the CS points, say, at the third entry in the GDT and those two-bits in this entry contain 0b11, the CPU executes instructions at ring 3.

Switching the privilege level

Switching the privilege level requires a bit more work than just updating CS. The easiest way to force the CPU to pick up the new settings is to raise a software interrupt (technically, there is an alternative called a far jump that we will not discuss in detail). The beauty of this is that a piece of code executing in user mode can raise an interrupt to reach ring 0, but this interrupt will execute a well defined code, namely the interrupt service handler, which again can be set up only while being in ring 0. So at startup, the operating system – executing at ring 0 – can set up the interrupt service handler to point to specific routines in the kernel, and later, during normal operations, a program executing in user mode can at any time call into the kernel by raising a software interrupt, for instance in order to read from the hard drive. However, a user mode program can only execute the specified interrupt service handler and is not able to execute arbitrary code at ring 0. Thus user mode and kernel mode are separated, but the interrupt service handlers provide specific gates to switch forth and back.

To make this work, the operating system needs to let the CPU know where each interrupt service handler is located. In protected mode, this is the purpose of the interrupt descriptor table (IDT) which an operating system needs to prepare and which contains, for each of the theoretically possible 256 interrupt service handlers, the address of the interrupt service handler as well as additional information, for instance which code segment to use (which will typically point to ring 0 to execute the interrupt in kernel mode).

My toy operating system ctOS, for instance, uses the interrupt 0x80 for system calls. A program that wants to make a system call puts a number identifying the system call into a specific register (EAX) and then raises interrupt 0x80. The interrupt service handler evaluates EAX and branches into the respective system call handler, see the ctOS system call handler documentation for more details.

Interrupts can not only be used to switch from user mode to kernel mode, but also for the way back. In fact, whenever the CPU returns from an interrupt service handler, it will return to the ring at which the execution was interrupted, using the stack to bring back the CPU into its original state. In order to move from ring 0 to ring 3, we can therefore prepare a stack that looks like being the stack arranged by the CPU if an interrupt occurs, and then execute the IRET instruction to simulate returning from an interrupt service handler.

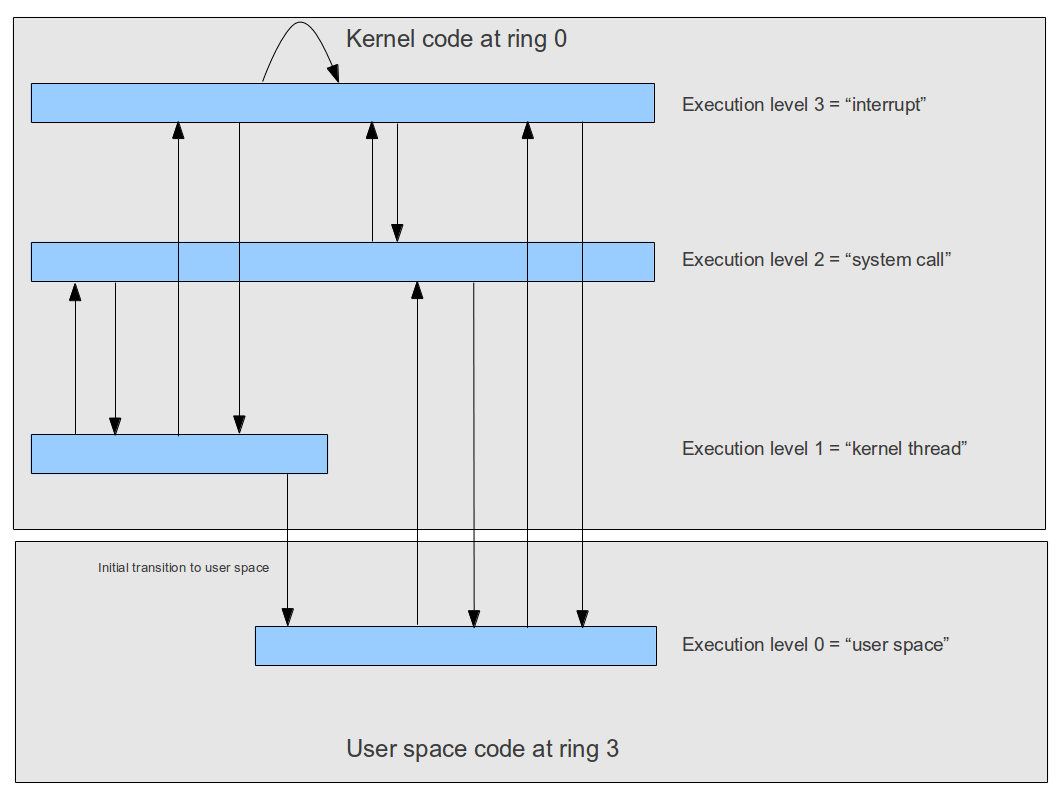
Matters get a bit more complicated by the fact that an interrupt service handler can in turn be interrupted by another interrupt, and that an operating system might want to implement kernel level threads which run outside of an interrupt context quite similar to a thread in user mode. To differentiate between those different situations, ctOS uses the concept of an execution level which is a software-maintained number describing the current context, as visualized below.

Memory model in protected mode

Another major change that the protected mode introduced into the x86 architecture was a more complex, but also more flexible memory model. To understand this, let us see how the older 8086 CPU handled memory (which is the mechanism that all modern Intel CPUs still use when being in real mode).

The 8086 was a 16-bit CPU, meaning that its registers were 16 bits wide. Therefore, a command like “put 0x10 into the memory location referenced by register AX” could only address 2¹⁶=65536 different memory locations. To be able to address more memory, the Intel engineers therefore came up with a trick. When memory was accessed, the content of two registers was used. In the example above, this would be AX (16 bits) and the code segment register CS, which has 16 bits as well. To determine the actual memory location, the content of the CS register was shifted left by four bits and then added to the content of AX. Thus, if, for instance, AX contained 0x200 and CS contained 0x100, the address would be

(0x100 << 4) + 0x200 = 0x1000 + 0x200 = 0x1200

This addressing mode is sometimes called segmentation because we can think of it as dividing the memory space into (overlapping) segments of 64 kByte and the CS register as selecting one segment.

Using segmentation, the 8086 CPU could address a bit more than 1 MB of memory and thus work around the limitations of a 16 bit CPU. With a 32 bit CPU, this is not really needed any more, but the 80386 nevertheless expanded on this idea and came up with a bit more complicated model.

In fact, in protected mode, there are three different types of addresses which can be used to describe the location of a specific byte in memory.

The first type of address is the logical address. Similarly to real mode, a logical address consists of a segment selector (16 bit) which specifies the memory segment the byte is located in and an offset (32 bit) which specifies the location of the memory space within the segment.

A program running in user mode usually only sees the offset – this is what appears for instance if you dump the value of a pointer in a user mode C program. The segment selector is set by the operating system and usually not changed by a user mode program. So from the programs point of view, memory is entirely described by a 32 bit address and hence appears as a 4 GB virtual address space.

When accessing memory, the CPU uses the global descriptor table to convert this logical address into a linear address which is simply a 32 bit value. This is similar to real mode where the segment and offset are combined into a linear 20 bit wide address, with the difference that the base address of the segment is not directly taken from the CS register but the CS register only serves as pointer into the GDT that holds the actual base address.

Logical and linear address are still virtual addresses. To convert the linear address into a physical address, the CPU finally uses a page table directory and a page table as explained in one of my last posts. When the CPU has first been brought into protected mode, paging is still disabled, so this final translation step is skipped and linear and physical address are the same. Note, however, that the translation between logical and linear address cannot be turned off and is always active. So setting up this translation mechanism and in particular the GDT is one of the basis initialization step which needs to be done when switching to protected mode.

Support for hardware multi-tasking

Apart from privilege levels and virtual memory, there is even more that the protected mode can do for you. In fact, the protected mode offers hardware support for multi-tasking.

Recall from my post on multi-tasking that a task switch essentially comes down to storing the content of all registers in a safe place and restoring them later. In the approach presented in my post, this is done by manually placing the registers on a stack. However, the x86 protected mode offers an alternative – the task state segment (TSS). This is an area of memory managed by the CPU that fully describes the state of a task. An operating system can initiate a task switch, and the CPU will do all the work to reload the CPU state from the TSS.

However, this mechanism is rarely used. It has a reputation of being slower than software task switching (though I have never seen any benchmarks on this), it introduces a lot of dependencies to the CPU and I am not aware of any modern operating system using this mechanism (Linux apparently used it in early versions of the kernel). Still, at least one TSS needs to be present in protected mode even if that mechanism is not used, as the TSS is also used to store some registers when an interrupt is raised while executing in ring 3 (see the corresponding section of the ctOS documentation for more details).

Long mode

Having followed me the long and dusty road down to an understanding of the protected mode, this one will shock you: protected mode is legacy.

In fact, the protected mode as we have discussed it is a 32 bit operating mode. Since a few years, however, almost every PC you can buy is equipped with a 64 bit CPU based on the x86-64 architecture. This architecture is fully backwards compatible, i.e. you can still run a protected mode operating system on such a PC. However, this does not allow you to address more than 4 GB of memory, as pointers are limited to 32 bit.

In long mode, the CPU uses 64 bit registers and is able to use 48 bit addressing, which is good enough for 256 TB of RAM.

Fortunately, if you understand the protected mode, getting used to long mode is not too difficult. The basis concepts of the various tables that we have discussed (page tables, the IDT and the GDT) remain unchanged, but of course the layout of these tables changes to accommodate for the additional address bits. The register set, however, changes considerably. The general purpose registers are extended to 64 bits and are renamed (RAX instead of EAX etc.). In addition, a few new registers become available. There are eight additional integer registers (R8 – R15) – which are typically used to pass arguments to subroutines instead of using the stack for this purpose – and eight more SSE registers.

Apart from that, long mode is just another mode of the x86 CPU family. And this is not the end of the story – there is unreal mode, there is virtual 8086 mode, there is the system management mode and there are new modes (“VMX root mode”) that support virtualization. If you want to learn more, I recommend the excellent OSDev Wiki – maybe the most valuable single OSDev site out there – and of course the Intel Software Developer manuals. Good luck!

Navigating downhill: the quantum variational eigensolver

In quantum mechanics, the dynamics of a system is determined by its Hamiltonian, which is a hermitian operator acting on the Hilbert space that describes the system at hand. The eigenstates and eigenvalues of the Hamiltonian then correspond to stationary states and their energies, and finding these eigenstates and the corresponding eigenvalues is the central task in computational quantum mechanics.

Unfortunately, in most cases, this is very hard. First, the Hilbert space of most physically relevant systems is infinite-dimensional. However, even if we are able to approximate the Hamiltonian by a hermitian operator acting on a finite dimensional subspace, finding the eigenvalues and eigenstates by applying classical methods from numerical linear algebra like the QR method is computationally challenging due to the high dimensional spaces involved. It is natural to ask whether a quantum computer can help.

In fact, there are several methods available for finding eigenvalues of a hermitian matrix on a quantum computer. In 1995, A. Kitaev described an algorithm which is now known as the quantum phase estimation (see [2] and [3]) which can be used to estimate eigenvalues of unitary matrices (and can be applied to hermitian matrices as well noting that if A is a hermitian matrix, U = e^iAt is unitary and that there is an obvious relation between the eigenvalues of U and A). Unfortunately, this algorithm might require a large number (millions or even billions) of fault-tolerant quantum gates which is currently completely out of reach. This is the reason why a second algorithm which was first described in [1] and is designed to run on a quantum computer with a low number of qubits attracted a lot of attention. This algorithm, called the variational quantum eigensolver, might be able to deliver improvements over what is possible with classical hardware with somewhere between a few tens and one hundred qubits.

Setup and preliminaries

To explain the approach, let us assume that we are given a quantum register with n qubits and some hermitian operator H acting on the corresponding 2ⁿ-dimensional Hilbert space. We assume further that we can write our operator as a linear combination

$H = \sum_i h_i H_i$

of a small number of operators H_i which correspond to measurements that we can easily implement. An example could be a decomposition

$H = \sum_i h_i P_i$

where each P_i is a tensor product of Pauli matrices (it is not difficult to see that such a decomposition exists for every hermitian operator. First, write the operator as a linear combination of projections $|x_i \rangle \langle x_i |$ and the vectors as linear combinations of tensor products to show that each hermitian operator is a linear combination of tensor products of hermitian single-qubit operators, and then use the fact that each hermitian single qubit operator is a linear combination of Pauli matrices). A tensor product of Pauli matrices corresponds to a measurement that can be easily implemented by a combination of a measurement in the standard computational basis and a unitary transformation, see for instance this discussion of Pauli measurements.

Now if the operators H_i correspond to measurements that can efficiently be implemented, it is also possible to efficiently evaluate the expectation value

$\langle H_i \rangle = \frac{\langle \psi | H_i | \psi \rangle }{\langle \psi | \psi \rangle}$

for a given state $|\psi \rangle$ , assuming that we can efficiently prepare the state N times and then conduct N independent measurements – in fact, if N is sufficiently large, the expectation value will simply be the average over the measurements (see [4], section IV, for a more detailed discussion) – here we see a trade-off between the number of times we need to prepare the state $|\psi \rangle$ and measure and the resulting precision.

Once we are able to measure the expectation value of each H_i, we can easily obtain the expectation value of H as the weighted average

$\langle H \rangle = \sum h_i \langle H_i \rangle$

A second observation that we need in order to understand the variational quantum eigensolver is the fact that the problem of finding the eigenvalues can be reduced to a variational problem. In fact, suppose that we are given a hermitian matrix A on a finite dimensional Hilbert space with eigenvalues $\lambda_1, \lambda_2, \dots$ . Let us order the eigenvalues (which are of course real) such that $\lambda_1 \leq \lambda_2 \leq \dots$ , and let us assume that $|\psi_1 \rangle, |\psi_2 \rangle \dots$ is an orthonormal basis of corresponding eigenvectors.

If we are now given an arbitrary non-zero vector $|\psi \rangle$ , we can of course expand this vector as a linear combination

$|\psi \rangle = \sum_i a_i |\psi_i \rangle$

which immediately gives us the following expression for the expectation value

$\langle A \rangle = \frac{1}{\langle \psi | \psi \rangle} \sum_i |a_i|^2 \lambda_i$

Given the ordering of the eigenvalues, we can now estimate this number as follows.

$\langle A \rangle = \frac{1}{\langle \psi | \psi \rangle} \sum_i |a_i|^2 \lambda_i \geq \frac{1}{\langle \psi | \psi \rangle} \sum_i |a_i|^2 \lambda_1 = \lambda_1$

It is also obvious that we have equality if $|\psi \rangle$ is actually an eigenvector of A with eigenvalue $\lambda_1$ . Thus finding an eigenvector for the lowest eigenvalue of A is equivalent to minizing the expectation value of A!

This is at the heart of many variational methods like the Ritz method that have always been part of the toolset of computational quantum mechanics. In most of these methods, one considers state vectors parametrized by a finite dimensional parameter set, i.e. states of the form $|\psi(\Theta) \rangle$ where the parameter $\Theta$ ranges over some subset of a finite dimensional euclidian space. One then tries to minimize the expectation value

$\langle H \rangle (\Theta) = \frac{\langle \psi(\Theta) | H | \psi(\Theta) \rangle}{\langle \psi(\Theta) | \psi(\Theta) \rangle}$

using classical methods from mathematical optimization. The state vector minimizing this expectation value is then taken as an approximation for an eigenvector of H for its lowest eigenvalue.

Many classical optimiziation approaches that one might want to employ for this task work iteratively. We start with some value of the parameter $\Theta$ , then determine the expectation value, adjust the parameter, determine the next expectation value and so forth. Unfortunately, calculating the expectation value of a matrix in a high dimensional Hilbert space is computationally very hard, which makes this algorithm difficult to apply to quantum systems with more than a few particles.

The algorithm

This is the point where the quantum variational eigensolver comes into play. If the operator H can – as assumed above – be decomposed into a sum of operators for which finding the expectation value can efficiently be done, then we can efficiently determine the expectation value of H as well and can use that in combination with a classical optimization algorithm to find an approximate eigenvector for H.

More precisely, here is the outline of the variational quantum eigensolver algorithm.

Decompose the operator H as a linear combination $H = \sum_\alpha h_\alpha H_\alpha$ where the expectation value of each $H_\alpha$ can be efficiently determined
Choose an initial value for the parameter $\Theta$
Prepare the quantum computer in the state $|\psi(\Theta) \rangle$
For each $H_\alpha$ , use measurements to determine the expectation value $\langle H_\alpha \rangle$
Calculate the expectation value of H as the weighted average $\langle H \rangle = \sum_\alpha h_\alpha \langle H_\alpha \rangle$
Apply a classical optimization step to determine a new value for the parameter $\Theta$
Start over with step 3 and repeat

So the algorithm switches forth and back between a quantum part – preparing the state and finding the expectation values – and a classical part, i.e. performing the actual optimization, and is therefore a prime example for a hybrid approach. This is visualized in the diagram below (which is a variation of the diagram presented in [1]).

Of course, to fully specify this algorithm, we have to define a method how to prepare the states efficiently and need to pick a classical optimization algorithm. In [1], the so-called coupled cluster method is chosen to prepare a state. In this method, the prepared state is given by applying a (parametrized) unitary transformation to a fixed reference state, and this unitary transformation can be efficiently implemented on a quantum computer. As an optimization algorithm, the downhill simplex method, also known as the Nelder-Mead method, is employed.

As noted in [1], the algorithm makes a certain trade-off between the number of iterations required to estimate the expectation values and perform the optimization step and the time required to run a single iteration on the quantum device. One of the main problems that todays quantum computers face, however, is to keep a quantum state stable over a longer period of time. Therefore the bottleneck is the run time or the number of operations that we spend in the quantum part of the algorithm, which this approach tries to minimize. As explained in [4], the variational principle also remains valid if we consider quantum systems with noise, which is an indication that the algorithm is comparatively resistant to noise. All this makes the quantum variational eigensolver a good candidate for a true quantum advantage on a near-term, noisy and not fully fault-tolerant quantum device.

Applications in computational chemistry

So far we have implicitly dealt with Hamiltonians H on a Hilbert space representing a quantum register, i.e. a tensor product of one qubit systems. For applications, there is therefore one additional step that we need to carry out in order to be able to apply the algorithm – we need to map the system and the Hamiltonian in question to an n-qubit quantum system. This involves in particular a projection of the (typically) infinite dimensional Hilbert space of the original problem onto a finite dimensional system.

A prime example that is detailed in [4] and in [1] is the Hamiltonian describing an atom with N electrons and their interactions with the nucleus and other electrons. Finding the eigenstates and eigenvalues of this Hamiltonian is known as the electronic structure problem.

In general, this is a difficult problem. Of course, the easiest case of this – the hydrogen atom – can be solved analytically and is treated in most beginner courses in quantum mechanics. However, already for the Helium atom, no closed solution is known and approximations have to be used.

In order to apply the variational quantum eigensolver to this problem, a mapping to a Hilbert space describing a quantum register needs to be done. As explained in [1], this can be done using the mechanism of second quantization and the Jordan-Wigner transform. In this paper, the authors have applied the method to estimate the strength of the chemical bond in a helium hydride ion HeH⁺, which is formed by the reaction of a proton with a helium atom. They show that in order to obtain a very good approximation, a four-dimensional Hilbert space is sufficient, so that the algorithm can be carried out on a quantum computer with only two qubits. Recently ([5]), this has been extended to a six-qubit system used to estimate the ground state energy of a BeH₂ molecule. Of course these are still comparatively small systems, but these experimental results encourage the hope that the approach scales and can be used on medium scale near-term quantum devices to go beyond what is possible with classical computers.

This work is also described in a post on the IBM website. IBM has made the Python sourcecode for similar applications available as part of its QISKit quantum computation library, so that everybody with a Q Experience account can run the algorithm and play with it. QISKit is a very interesting piece of software, and I will most likely devote one or more future posts on QISKit and similar frameworks like pyQUIL.

References

1. A. Peruzzo et. al., A variational eigenvalue solver on a photonic quantum processor, Nature Communications volume 5 (2014), available at www.nature.com/articles/ncomms5213
2. A. Kitaev, Quantum measurements and the Abelian Stabilizer Problem, arXiv:quant-ph/9511026
3. R. Cleve, A. Ekert, C. Macchiavello, M. Mosca, Quantum Algorithms Revisited, arXiv:quant-ph/9708016
4. J. R. McClean, J. Romero, R. Babbush, A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, arXiv:1509.04279
5. A. Kandala, A. Mezzacapo, K. Temme,
M. Takita, M. Brink, J. M. Chow, J. M. Gambetta, Hardware-efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets, Nature volume 549, pages 242–246 (14 September 2017), available as arXiv:1704.05018v2

Into the quantum lab – first steps with IBMs Q experience

Even though physical implementations of quantum computers make considerable progress, it is not likely that you will have one of them under your desk in the next couple of years. Fortunately, some firms like IBM and Rigetti have decided to make some of their quantum devices available only so that you can play with them. In this post, we will have a first look at IBMs cloud offering – the IBM Q experience.

IBM offers different ways to interact with their quantum computers. The easiest access is provided by the interactive composer which allows you to create a quantum circuit online and to run it on a 5 qubit quantum computer based on superconducting qubits after registering.

The screenshot below shows the editor screen. At the top, you find an overview of the available quantum devices, both realising five (physical) qubits, and some of the main characteristics like error rates and decoherence times.

In the lower area of the screen, you can compose quantum circuits graphically. You can add quantum gates that manipulate the five qubits q[0] – q[4] and measurements. After setting up your circuit, you can either simulate the circuit or you can run it on the actual device. It is also possible to export the circuit as a QASM code snippet and to save experiments and results as so-called quantum scores.

Let us now run this circuit on the actual quantum hardware. Doing this consumes units, i.e. credits. A standard run consists of 1024 repetitions and one measurement after each repetition and consumes three units (which are replenished after the execution has completed). The execution is queued and, typically after a few minutes, the results are made available online (and you receive a mail informing you about the execution). When running a circuit, the platform also checks whether that circuit was executed before (by you our someone else) and if yes offers you immediate access to the previous results without consuming any units. The screenshot below shows the result of one of these runs.

The interesting part is the diagram at the top that shows the measurement outcomes in the computational basis, i.e. for each member of the computational basis on the x-axis, the value shows the percentage of measurements having that basis element as result. In this example, we see that almost always, the result is 00000, as expected from the circuit in which we do a double inversion of the first qubit. However, in some cases – corresponding to 1,3 percent of all runs – the outcome is 00001. This is a nice example for an error that occurs whenever we switch from a simulator to a real physical device. Note that in the IBM Q experience, the qubit q[0] is the least significant qubit and the rightmost qubit in the notation of the computational basis.

Now let us try something else – we want to put our system into an equal superposition

$\sum_i |i \rangle$

which is the usual starting point for most quantum algorithms. We know that we can achieve this by applying a Hadamard gate on each qubit. The following screenshot shows the resulting circuit for three qubits and the results of a (cached) run.

As expected, we see that our measurement results are spread across eight (2³) vectors of the computational basis. However, we also see that again, the result does not exactly match the theoretical prediction – the values are not exactly equally distributed but we see slight deviations as before.

Finally, let us try out a multi-qubit gate. The screenshot below shows the result of a run with two CNOT gates. The first CNOT gate receives a logical one on its control bit, the second CNOT gate a logical zero. Thus, the result should be 00011, i.e. the first (least significant) qubits are inverted. In reality, we again get this result plus some noise, represented by unexpected outcomes in the measurements.

Playing with the composer is fun, and makes it easy to create simple circuits from scratch. However, more complicated circuits soon become difficult to define in this way. For those circuits, the IBM platform offers an API that can be used to run experiments using Python scripts that can much easier be developed and debugged step by step. We will look at this option in a later post. Until then, I recommend you get an account and create some circuits yourself – happy hacking!

Virtual memory

If you wanted a slogan that summarizes key trends in the IT industry over the last 30+ years, then “everything is virtual” would be a good candidate. In todays computing environments, essentially every physical resource is virtualized – and pretty much the first resource where this happened in mainstream computing was memory. In this post, we will look a bit into virtual memory: what it is, how it is implemented and how it is used.

To introduce the concept, suppose you were running a document storage service. Maybe you own a large warehouse with thousands of little boxes, and customers can hand in envelopes with documents that you will then safely store in one of the boxes. Obviously, you need a smart way to manage all these little envelops and boxes.

The first approach that someone might come up with is very simple. Suppose that your warehouse contains 10.000 boxes and each box can store one envelope. You could then number the boxes, say from zero to 9.999, and ask customers to label their envelops with numbers in that range. When a customer hands in an envelope that has, say, 11 on it, then an agent accepts the envelope and simply puts it into the box that has exactly that number, i.e. 11 in this case.

In the world of computing, this is how physical memory addresses work. Of course, the agent corresponds the memory controller and the customer to the CPU. When the CPU wants to store some data in memory, it passes that data (the envelope) along with the address where the data should be stored to the memory controller, and the memory controller stores the data at the requested address.

That model is simple, and the first customer will love it – the customer can freely decide about where the envelope should be placed, and feels like owning the entire warehouse exclusively.

However, suppose you are the second customer. If, for some reason, you also want to store an envelope in box 11, there is a problem as this box is already taken. Similar problems are caused by physical memory addressing if you want to implement multitasking, i.e. allow several programs (customers) to use resources of the PC (i.e. memory) simultaneously. If, for instance, you want to run two programs that are both designed to start at address 0x100 in memory, the first program will properly load and execute, but it will consume this area of memory and you will not be able to load and run the second program. This is the mode that most early CPUs used, for instance the 8086 used in the first IBM PCs (and todays CPUs still start in the so-called real mode that uses the same addressing pattern with a bit of a twist).

So for multitasking, you need a different model. Let us look at our warehouse again. Instead of just storing the envelope in the box designated by the label on the envelope, the agent could, for each and every customer, maintain a mapping table. When a customer hands in an envelope, say again with label 11, the agent would locate an unused box. This can have any label, say it is 3. The agent would then add an entry to the mapping table that maps – for this customer – label 11 to box 3, and store the envelope in box 3. If a second customer also hands in an envelope with label 11, the agent would add a similar entry to the mapping table for this customer, this time mapping 11 to – say – box 7

Similarly, if a customer requests to retrieve an envelope, say again envelope 11, the agent would consult the mapping table for this specific customer and see that the envelope is located in box 3, so that it can be located and handed over to the customer. The agent could then either mark the box as unused again or agree with the customer to reserve the space for later use.

Of course, this requires some overhead – the agent needs to maintain mapping tables, one table per customer. But assuming that there is still enough space left in the warehouse, every customer still feels like owning the entire warehouse – in fact, the customer is not even able to detect a difference to the first system. And there are more interesting opportunities that the system offers. If, for instance, a new customer arrives but the warehouse is full, the agent could locate a box that has not been used for a while, transfer the content of this box into some other storage room and use the box again.

Translated back to the world of computing, this model corresponds to virtual memory addresses. In that model, an additional translation unit sits between the CPU and the memory controller. This unit uses a system of mapping tables – called the page tables – to map forth and back between virtual and physical addresses. An operating system implements one different set of tables, i.e. a different mapping, for each process. Thus each process is like the customer in our warehouse example and logically can access the entire virtual memory space, even if other processes run at the same time. The operating system can even swap out areas of memory, i.e. if physical memory is exhausted, it could copy parts of its content onto a slower medium, say the hard drive, and reallocate that space – a mechanism which is usually called swapping.

There is much more that we can do having virtual memory at our disposal. We could, for instance, implement a mechanism called copy-on-write. Suppose that you wanted to copy a large area of physical memory which can be quite time consuming. Instead of copying, you could simply adapt the address mapping such that different virtual addresses point to the same physical address. For the CPU, which only sees virtual addresses, it appears like if the content had copied – until, of course, the CPU tries to change the copy. So the operating system needs to listen for writes into this memory area, and only if that write takes place create an actual physical copy. If we are lucky, only a comparatively small area of the copied memory is actually written to, and then copy-on-write can be much more efficient in terms of performance and overall memory utilization than a plain physical copy.

Designing the structure of the mapping tables requires some care. Of course, we cannot map every single byte of memory – storing that mapping information alone would consume the entire system memory. Instead, the memory is divided into small chunks called pages. Traditionally, a page is 4096 bytes, but other page sizes are feasible. We then map page by page, i.e. for each page, we map its starting address in virtual address space to a corresponding physical page.

In fact, this mapping is usually organized as a hierarchy of page tables, with the lowest level being the so-called page table directory. Each page table has 1024 entries, each of which describes the mapping of one page, so each page table is able to hold the mapping for 4 MB of memory. Thus we need 1024 page tables to describe the full address space accessible with 32 bits. The page table directory is then another table that simply holds the address of these 1024 page tables, as illustrated below.

In practice, there is not only one page table directory, but several page table directories, such that each process uses a different set of page table and hence a different mapping of physical and virtual addresses, i.e. a different virtual address space. In fact, for most operating systems, a process and an address space are almost synonyms. For Unix like operating systems, each process has a separate address space, but all threads running within this process share this address space which is an important conceptual difference between threads and processes.

To be able to use several page table directories, we need a way to switch between them. On the x86 platform, this is done by loading the address of the page table directory into a special register of the CPU called CR3. When we switch forth and back between two threads or tasks that do not belong to the same process, the operating system needs to make sure that the register CR3 is loaded with the address of the new page table directory corresponding to the process to which we switch. As every process has its own virtual-to-physical address mapping, the address spaces of two different processes are very effectively isolated and we can make sure that process A does not read or write memory allocated by process B and vice versa.

There is one problem, though. Changing the value of CR3 is, at the end of the day, an ordinary instruction. If every process could execute this instruction, a process could reload CR3 with a pointer to a manipulated page table. Thus, every process would be able to change the mapping between virtual and physical memory, effectively destroying the isolation.

The solution is to introduce privilege levels. Each process is running at one of these levels, and the operating system is running at the highest level. We could then make the instructions that manipulate CR3 privileged instructions that only the operating system is allowed to execute, and thus only the operating system could change page tables. These different privilege levels have been introduced into the x86 architecture as part of the protected mode that is also required to implement virtual memory and which will be the topic of one of the next posts in this series.

Shor’s quantum factoring algorithm

Until the nineties of the last century, quantum computing seemed to be an interesting theoretical possibility, but it was far from clear whether it could be useful to tackle computationally hard problems with high relevance for actual complications. This changed dramatically in 1994, when the mathematician P. Shor announced a quantum algorithm that could efficiently solve one of the most intriguing problems in applied mathematics – factoring large numbers into their constituent primes, which, for instance, can be used to break commonly used public key cryptography schemes like RSA.

Shor’s algorithm is significantly more complicated than the quantum algorithms that we have studied so far, so we start with a short overview and then look at the individual pieces in more detail.

Given a number M that we want to factorize, the first part of Shor’s algorithm is to find a number x which has no common divisor with M so that it is a unit modulo M. In practice, we can just guess some x and compute the greatest common divisor gcd(x,M) – if this is not one, we have found a factor of M and are done, if this is one, we have the number x that we need. This step can still be done efficiently on a classical computer and does not require a quantum computer.

The next part of the algorithm now uses a quantum algorithm to determine the period of x. The period is the smallest non-zero number r such that

$x^r \equiv 1 \mod M$

The core of this step is the quantum algorithm that we will study below. However, the quantum algorithm does not exactly return the number r, but it returns a number s which is close to a multiple of $\frac{N}{r}$ , where N is a power of two. Getting r out of this information is again a classical step that uses the theory of continued fractions. The number N that appears here is N = 2ⁿ where n is the number of qubits that the quantum part requires, and needs to be chosen such that M² can be represented with n bits.

Finally, the third part of the algorithm uses the period r to find a factor of M, which is again done classically using elementary number theory. Thus the overall layout of the algorithm is as follows.

Find the smallest number n (the number of qubits that we will need) such that $M^2 \leq N = 2^n$ and a number $x < M$ such that gcd(x,M) = 1
Use the quantum part of the algorithm to find a number s which is approximately an integer multiple of N / r
Use the theory of continued fractions to extract the period r from this information
Use the period to find a factor of M

We will know look at each of these steps in turn (yes, this is going to be a bit of a lengthy post). To make this more tangible, we use a real example and assume that we wanted to factor the number M = 21. This is of course a toy example, but it allows us to simulate and visualize the procedure efficiently on a classical computer.

Determine n and x

The first step is easy. First, we need to determine the number n of qubits that we need. As mentioned above, this is simply the bit length of M². In our case, M² = 441, and the next power of two is 512 = 2⁹, so we need n = 9 qubits.

The next step is to find the number x. This can easily be done by just randomly picking some x and checking that is has no common prime factor with M. In our example, let us choose x = 11 (which is a prime number, but this is just by accident and not needed). It is important to choose this rather randomly, as the algorithm might fail in some rare instances and we need to start over, but this only makes sense if we do not pick the same choice again for our second trial.

The quantum part of the algorithm

Now the quantum part of the algorithm starts. We want to calculate the period of x = 11, i.e. the smallest number r such that x^r – 1 is a multiple of M = 21.

Of course, as our numbers are small, we could easily calculate the period classically by taking successive powers of 11 and reducing modulo 21, and this would quickly tell us that the period is 6. This, however, is no longer feasible with larger numbers, and this is where our quantum algorithm comes into play.

The algorithm uses two quantum registers. The first register has n qubits, the second can have less, in fact any number of qubits will do as long as we can store all numbers up to M in it, i.e. the bit length of M will suffice. Initially, we bring the system into the superposition

$\frac{1}{\sqrt{N}} \sum_k |k \rangle |0 \rangle$

which we can for instance do by starting with the state with all qubits being zero and then applying the Hadamard-Walsh transformation to the first register.

Next, we consider the function f that maps a number k to x^k modulo M. As for every classical function, we can again find a quantum circuit U_f that represents this function on the level of qubits and apply it to our state to obtain the state

$\frac{1}{\sqrt{N}} \sum_k |k \rangle |x^k \mod M \rangle$

In his original paper [2], Shor calls this part the modular exponentiation and shows that this is actually the part of the quantum algorithm where most gates are needed (not the quantum Fourier transform).

This state has already some periodicity built into it, as x^k modulo M is periodic with period r. If we could measure all the amplitudes, we could easily determine r. However, every such measurement destroys the quantum state and we have to start again, so this algorithm will not be very efficient. So again, the measurement is an issue.

Now, Shor’s idea is to solve the measurement issue by first applying (the inverse of) a quantum Fourier transform to the first register and then measure the first register (we apply the inverse of the quantum Fourier transform while other sources will state that the algorithm uses the quantum Fourier transform itself, but this is just a matter of convention as to which transformation you call the Fourier transform). The outcome s of this measurement will then give us the period!

To get an idea why this is true, let us look at a simpler case. Assume that, before applying the quantum Fourier transform, we measure the value of the second register. Let us call this value y. Then, we can write y as a power of x modulo M. Let k₀ be the smallest exponent such that

$x^{k_0} = y$

Then, due to the periodicity, all values of k such that x^k = y modulo M are given by

$k = k_0 + jr$

Here the index j needs to be chosen such that k₀ + jr is still smaller than M. Let A denote the number of possible choices for j. Then, after the measurement, our state will have collapsed to

$\frac{1}{\sqrt{A}} \sum_{j=0}^{A-1} |k_0 + jr \rangle |y \rangle$

Let us now apply the inverse of the quantum Fourier transform to this state. The result will be the state

$\frac{1}{\sqrt{AN}} \sum_{j=0}^{A-1} \sum_{s=0}^{N-1} \eta^{(x_0 + jr)s} |s \rangle$

Now let us measure the first register. From the expression above, we can read off the probability P(s) to measure a certain value of s – we just have to add up the squares of all amplitudes with this value of s. This gives us

$P(s) = \frac{1}{AN} \big| \sum_{j=0}^{A-1} \eta^{jrs} \big|^2$

This looks complicated, but in fact this is again a geometric series with coefficient $q = \eta^{rs}$ . To see how the value of the series depends on s, let us assume for a moment that the period divides N (which is very unlikely in practice as N is a power of two, but let us assume this anyway just for the sake of argument), i.e. that N = r u with the frequency u being an integer. Thus, if s is a multiple of u, the coefficient q is equal to one (as $\eta^N = 1$ ) and the geometric series sums up to A, giving probability 1 / N to measure this value. If, however, s is not a multiple of u, the value of the geometric series is

$\frac{1 - q^A}{1 - q}$

But in our case, A is of course simply equal to u, and therefore q^A is equal to one. Thus the amplitude is zero! We find – note the similarity to our analysis of the Fourier transform of a periodic sequence – that P(s) is sharply peaked at multiples of $u = \frac{N}{r}$ !

We were able to derive this result using a few simplifications – an additional measurement and the assumption that the frequency is an integer. However, as carried out by Shor in [2], a careful analysis shows that these assumptions are not needed. In fact, one can show (if you want to see all the nitty-gritty details, you could look at Shor’s paper or at my notes on GitHub that are based on an argument that I have seen first in Preskill’s lecture notes) that with reasonably high probability, the result s of the measurement will be such that

$\big| \{sr\}_N \big| \leq \frac{r}{2}$

where $\{sr\}_N$ denotes the residual of sr modulo N. Intuitively, this means that with high probability, the residual is very small, i.e. rs is close to a multiple of N, i.e. s is close to a multiple of N / r. In other words, it shows that in fact, P(s) has peaks at multiples of N / r.

The diagram below plots the probability distribution P(s) for our example, i.e. N = 512 and r = 6 (this plot has been generated using the demo Shor.py available in my GitHub account which uses the numpy package to simulate a run of Shor’s algorithm on a classical computer)

As expected, we see sharp peaks, located roughly at multiples of 512 / 6 = 85.33. So when we measure the first register, the value s will be close to a multiple of 512 / 6 with a very high probability.

So the quantum algorithm can be summarized as follows.

Prepare a superposition $\frac{1}{\sqrt{N}} \sum_k |k \rangle |x^k \mod M \rangle$
Apply the (inverse of the) quantum Fourier transform to this state
Measure the value of the first register and call the result s

When running the simulation during which the diagram above was created, I did in fact get a measurement at s = 427 which is very close to 5*512 / 6.

Extracting the period

So having our measurement s = 427 in our hands, how can we use this to determine the period r? We know from the considerations above that s is close to a multiple of N / r, i.e. we know that there is an integer d such that

$\big| sr - dN \big| \leq \frac{r}{2}$

which we can rewrite as

$\big| \frac{s}{N} - \frac{d}{r} \big| \leq \frac{1}{2N} < \frac{1}{M^2}$

Thus we are given two rational numbers – s / N and d / r – which we know to be very close to each other. We have the first number s / N in our hands and want to determine the second number. We also know that the denominator r of the second number is smaller than M. Is this sufficient to determine d and r?

Surprisingly, the answer is “yes”. We will not go into details at this point and gloss over some of the number theory, but refer the reader to the classical reference [1] or to my notes for more details). The first good news is that two different fractions with denominators less than M need to be at least by 1 / M² apart, so the number d / r is unique. The situation is indicated in the diagram below.

But how to find it? Luckily, the theory of continued fractions comes to the rescue. If you are not familiar with continued fractions, you can find out more in the appendix of my notes or on the very good Wikipedia page on this. Here, we will just go through the general procedure using our example at hand.

First, we write

$\cfrac{427}{512} = 0 + \cfrac{1}{\cfrac{512}{427}} = 0 + \cfrac{1}{1 + \cfrac{85}{427}}$

We can do the same with 85 / 427, i.e. we can write

$\cfrac{85}{427} = \cfrac{1}{\cfrac{427}{85}} = \cfrac{1}{5 + \cfrac{2}{85}}$

which will give us the decomposition

$\cfrac{427}{512} = 0 + \cfrac{1}{1 + \cfrac{1}{5 + \cfrac{2}{85}}}$

Driving this one step further, we finally obtain

$\cfrac{427}{512} = 0 + \cfrac{1}{1 + \cfrac{1}{5 + \cfrac{1}{42 + \cfrac{1}{2}}}}$

This is called the continued fraction expansion of the rational number 427 / 512. More generally, for every sequence $[a_0 ; a_1, a_2, \dots ]$ , we can form the continued fraction

$a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \dots}}$

given by that sequence of coefficients, which is obviously a rational number. One can show that in fact every rational number has a representation as a continued fraction, and our calculation has shown that

$\cfrac{427}{512} = [0; 1,5,42,2]$

This sequence has five coefficients. Now given a number m, we can of course look at the sequence that we obtain by looking at the cofficients up to index m only. For instance, for m = 3, this would give us the sequence

$[0; 1,5,42]$

The rational number represented by this sequence is

$0 + \cfrac{1}{1 + \cfrac{1}{5 + \cfrac{1}{42}}} = \cfrac{211}{253}$

and is called the m-th convergent of the original continued fraction. We have such a convergent for every m, and thus get a (finite) series of rational numbers with the last one being the original number.

One can now show that given any rational number x, the series of m-th convergents of its continued fraction expansion has the following properties.

The convergents are in their lowest terms
With increasing m, the difference between x and the m-th convergent gets smaller and smaller, i.e. the convergents form an approximation of x that gets better and better
The denominators of the convergents are increasing

So the convergents can be used to approximate the rational number x by fractions with smaller denominator – and this is exactly what we need: we wish to approximate the rational number s / N by a ratio d / r with smaller denominator which we then know to be the period. Thus we need to look at the convergents of 427 / 512. These can be easily calculated and turn out to be

$0, 1, \cfrac{5}{6}, \cfrac{211}{253}, \cfrac{427}{512}$

The last convergent whose denominator is still smaller than M = 21 is 5 / 6, and thus we obtain r = 6. This is the period that we are looking for!

So in general, the recipe to get from the measured value s to r is to calculate the convergents of the rational number s / N and pick the denominator of the last convergent that has a denominator less than M. Again, if you want to see the exact algorithm, you can take a look at my script Shor.py.

Find the factor

We are almost done. We have run the quantum algorithm to obtain an approximate multiple of N / r. We have then applied the theory of continued fractions to derive the period r of x from this measurement. The last step – which is again a purely classical step – is now to use this to find a factor of M. This is in fact comparatively easy.

Recall that – by definition of the period – we get one if we raise x to the power of r and than reduce module M. In other words, x^r minus one is a multiple of M. Now assume that we are lucky and the period r is even. Then

$(x^{\frac{r}{2}} - 1)(x^{\frac{r}{2}} + 1) = (x^r - 1) \equiv 0 \mod M$

With a bit of elementary number theory, one can now show that this implies that the greatest common divisor gcd(x^r/2-1, M) is a factor of M (unless, in fact, x^r/2 is minus one modulo M, in which case the argument fails). So to get from the period to a potential factor of M, we simply calculate this greatest common divisor and check whether it divides M!

Let us do this for our case. Our period is r = 6. With x = 11, we have x³ = 1331, which is 8 module M. Thus

$\text{gcd}(x^{\frac{r}{2}} - 1 \mod M, M) = \text{gcd}(7,21) = 7$

which is the factor of M = 21 that we were looking for.

Performance of the algorithm

In our derivation, we have ignored a few special cases which can make the algorithm fail. For instance, suppose we had not measured s = 427, but s = 341 after applying the Fourier transform. Then the corresponding approximation to 341 / 512 would have been 4 / 6. However, the continued fraction algorithm always produces a result that is in its lowest terms, i.e. it would give us not 4 / 6, but 2 / 3. Looking at this, we would infer that r = 3, which is not the correct result.

There are a few other things that can go wrong. For instance, we could find a period r which is odd, so that our step to derive a factor of M from r does not work, or we might measure an unlikely value of s.

In all these cases, we need to start over and repeat the algorithm. Fortunately, Shor could show that the probability that any of this happens is bounded from below. This bound is decreasing with larger values of M, but it is decreasing so slowly that the expected number of trials that we need grows at most logarithmically and does not destroy the overall performance of the algorithm.

Taking all these considerations into account and deriving bounds for the number of gates required to perform the quantum part of the algorithm, Shor was able to show that the number of steps to obtain a result grows at most polynomially with the number of bits that the number M has. This is obviously much better than the best classical algorithm that requires a bit less than exponential time to factor M. Thus, assuming that we are able to build a working quantum computer with the required number of gates and qubits, this algorithm would be able to factorize large numbers exponentially faster than any known classical algorithm.

Shor’s algorithm provides an example for a problem that is believed to be in the class NP (but not in P) on a classical computer, but in the class BQP on a quantum computer – this is the class of all problems that can be solved in polynomial time with a finite probability of success. However, even though factorization is generally believed not to be in P, i.e. not doable in polynomial time on classical hardware, there is not proof for that. And, even more important, it is not proved that factorization is NP-complete. Thus, Shor’s algorithm does not render every problem in NP solvable in polynomial time on a quantum computer. It does, however, still imply that all public key cryptography systems like RSA that rely on the assumption that large numbers are difficult to factor become inherently insecure once a large scale reliable quantum computer becomes available.

References

1. G.H. Hardy, E.M. Wright, An introduction to the theory of numbers, Oxford University Press, Oxford, 1975
2. P. Shor, Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer, SIAM J.Sci.Statist.Comput. Vol. 26 Issue 5 (1997), pp 1484–1509, available as arXiv:quant-ph/9508027v2

How does multitasking really work?

The first PC on which I was running a copy of Linux back in the nineties did of course only have one CPU, so it was clear to me that it could physically only execute one instruction at a time – but still, it magically created the impression to run several programs in parallel without visible delay. How could that ever work? Almost twenty years later, I finally found the answer.

In fact, trying to understand how multitasking and multithreading actually work was one of my main motivations when I developed the ctOS kernel a couple of years ago. In this post, I will try to explain the basic mechanism behind the magic.

The basic idea sounds simple enough. Suppose a task has been running for some time and the operating system decides that it is time to switch to a different task. Then the operating system kernel will interrupt the current execution and save the current state of the CPU somewhere in memory. It then locates a different task that is ready to be run – a process which is called scheduling– and retrieves the saved CPU state representing this task from memory. Then, it will let the CPU continue execution with that saved state. As this state is exactly the state of the CPU that was in place when the newly scheduled task was stopped, the CPU will continue to process this task as if it had never been interrupted.

Unfortunately, this simple explanation leaves a number of questions open. First, if a task is executing, it means that the CPU is busy running this task. How, then, can the operating system “do” something? Second, what is the “state of the CPU”? How can we store it and how can we put the CPU back in a saved state? And then, how do we decide that “it is time to switch to a different task”? It turns out that the answer to these questions have to do with interrupts.

Task switching, interrupts and the stack

To explain this, let us for a moment assume a vastly simplified world where all tasks currently active do not require I/O operations. Suppose task A is currently being processed, i.e. the CPU is executing the stream of instructions (the “program”) that make up this task. At some point, we will see an interrupt firing. If there is no I/O, this is usually the timer interrupt that fires periodically, say one thousand times per second.

If this happens, the CPU will stop the execution of task A and start to execute an interrupt service handler. Now the interrupt service handler has been set up by the operating system and points at code within the operating system kernel – so at this point, control is given to the operating system! At the same time, we have learned that the CPU will store the value of some registers like EIP on the stack, and a smart interrupt handler will store the value of additional registers on the stack as well in order to be able to use and reconstruct their value later, and, right at its end, contain code to pop the register values off the stack again. So we could as well set up our ISR in such a way that it does in fact store the value of all registers on the stack. This already provides two ingredients for the task switching mechanism – a way to make sure that the operating system gains control of the CPU at least once a millisecond and a saved CPU state on the stack!

Now the operating system will usually maintain a list of tasks and scan that list according to certain criteria to find a task which should be executed next – we will look at this process in greater detail further below. Suppose that it determines a task which we call B which should be run next. For the sake of simplicity, let us also assume that this task is not entirely new, but has already been running for some time (setting up a new task is a bit more complicated). Thus, when task B was interrupted for the last time, its state was also saved on the stack somewhere, and our operating system has hopefully stored a pointer to this stack.

What we now want to do is to exchange the stored state of task A with that of B. The easiest way to do this is not to copy around the stacks, but to manipulate the stack pointer such that the execution resumes using the stack of task B instead of task A! When we do this and reach the end of the interrupt service handler, the part of the interrupt service handler that is responsible for popping all registers off the stack again as well as the final IRET will use the stack of task B. In other words, the CPU will pick up the state of task B instead the state of task A. It will therefore continue execution with the state of the registers and the instruction pointer that task B had when it was interrupted – in other words, task B will continue to execute instead of task A, and we have switched from task A to task B.

In reality, there are a few subtle points that need to be worked out in more detail when you really want to build this. You will have to think about what the stack actually is – does every task have its own stack, how do you isolate them etc. In addition, a task switch might invoke a switch to a different process and thus to a different virtual address space, so at some point, addresses become invalid and cannot be accessed any more. The exact process that ctOS uses is described in the section on task switching in the interrupt handling documentation of ctOS.

We have explained the process of task switching using the timer interrupt as an example. However, this is not the only possible trigger for a task switch. There are of course other hardware interrupts that might trigger a task switch, but more importantly, many task switches do in fact occur during a system call! Assume for instance that a task wants to read data from the hard drive. It will then invoke a system call to do this, i.e. it will hand over control to the kernel voluntarily. The kernel will ask the hard drive to go and get the data, but of course this takes some time. Thus the kernel will in general not return to this task, but schedule a different task and execute a task switch. If (as ctOS does it) a system call is itself implemented as a software interrupt, the mechanism is exactly the same as if a task switch had been done during the processing of a hardware interrupt (if the faster SYSENTER/SYSEXIT mechanism is used, the processing is a bit different but the idea is the same).

Scheduling

What we have not explained so far is how the operating system does actually select a new task to be executed. The exact details how to do this are different for each operating system, but it is probably fair to say that there are in general two main ingredients – the time the task has been running until the last task switch and the state of the task.

First, there is the CPU time that a task has consumed since the last task switch, commonly measured by the quantum. The quantum is a number that is set to some initial value when the task gets control of the CPU. During each processing of the timer interrupt, the quantum of the currently active task is decreased by one. As the timer interrupt fires periodically, the quantum thus measures the time that the task has already consumed – the lower the remaining quantum, the longer the task did already run. If a task has reached quantum zero, it might be a good idea to schedule a different task.

Second, there is the state of a task. Not every task is ready to be executed at any given point in time. A task might for instance be waiting for some event (user input, I/O, ..) or might otherwise be blocked. Our a task could be in the status new, indicating that it is currently still being set up and not yet ready to run. Or it might have been stopped by a signal and be waiting for the signal to continue. And finally, a task can either be active i.e. currently executing, or ready, i.e. waiting to be scheduled.

During scheduling, only tasks in status ready will be considered as candidates for execution. One way to implement scheduling is to put all ready tasks onto a queue, called the ready queue. Scheduling than basically proceeds as follows.

Check whether the currently active task has used up its quantum
If no, decrease the quantum by one and return – no task switch will be done. Otherwise proceed with the next step
Set the state of the currently active task to “ready”, set its quantum back to its initial value and queue the task at the end
Select the first task in the ready queue. Update its status to active and mark it as target of the next task switch

When a task that was not ready but, for instance, blocked, becomes ready, it is added at the end of the ready queue with an initial quantum.

There is a more advanced version of this simple algorithm called round-robin scheduling with dynamic priorities. In this model, there is more than one ready queue, in fact there is a list of priorities, say 0 – 15, and there is one queue for each priority. If a new task to be scheduled needs to be determined, these queues are scanned for candidates, starting with the highest priority queue. The priority can be adjusted at run-time based on the current behaviour of the process – see the documentation of the ctOS scheduler for more details. This approach is still comparatively simple, and designing a highly optimized scheduler is an art that can make the difference between a good and a lousy performance. Currently, Linux uses a different scheduling mechanism called CFS, but scheduling remains a tricky tasks, especially in an SMP environment, and we will probably see additional work going into this in the future (see for instance this article for a more in-depth discussion).

Now multi-tasking is nice, but to really execute several programs at the same time has an additional dimension – memory. If you want to run different programs on one physical machine that might even belong to different users, you need to make sure that a program cannot access memory reserved for a different program, i.e. you need some level of memory space isolation. Fortunately, modern CPUs offer a mechanism called virtual memory that we can use for this purpose and that we will explain in the next post.

The quantum Fourier Transform

We are getting closer to the most spectacular early quantum algorithm – Shor’s algorithm for factoring large composite numbers which can be used to break the most widely used public key cryptography systems. But before we can tackle this algorithm, there is one more thing that we need to understand – the quantum Fourier transform.

The discrete Fourier transform

Let us leave the quantum world for a few moments and take a look at a classical area in mathematics – the discrete Fourier transform. To motivate the definition to come, let us for a moment assume that we are observing a time dependent signal, i.e. a function f(t) depending on the time t. Let us also assume that we are interested in processing this signal further, using a digital computer. This will force us to reduce the full signal to a finite number of values, i.e. to a set of values f(0), f(1), …, f(N-1) at N discrete points in time.

Now assume that we wanted to calculate the classical Fourier transform of this function, i.e. the function $\hat{f}$ given by (the exact formula depends on a few conventions)

$\hat{f}(x) = \int_{-\infty}^{\infty} f(t) e^{-i x t} dt$

If we now replace the function f by the sum of those functions which have value f(i) over a range of length 1, i.e. by its discrete version, this formula turns into

$\hat{f}(x) = \sum_{t=0}^{N-1} f(t) e^{-i x t}$

Now we could code the discrete values f(0), f(1), .. as a sequence x_k of numbers, and we could apply the same process to the Fourier transform and replace it by a sequence X_k of numbers, representing again the values at the discrete points 0, 1, …. The above formula then tells us that these numbers would be given by

$X_k = \sum_{j=0}^{N-1} x_j e^{-i j k}$

We could now look at this formula as giving us an abstract mapping from the set of sequences of N numbers to itself, provided by (putting in a factor $2 \pi / N$ )

$X_k = \sum_{j=0}^{N-1} x_j e^{- \frac{2\pi i}{N} j k}$

This transformation is called the discrete Fourier transform.

There is a different way to look at this which is useful to derive some of the properties of the discrete Fourier transform. For every k, we can build the N-dimensional complex vector $u^k$ with components $u^k_n$ by setting

$u^k_n = e^{\frac{2\pi i}{N} k n}$

These vectors are mutually orthogonal with respect to the standard hermitian product. In fact, the product of any two of these vectors is given by

$(u^k u^{k'})^* = \sum_{j=0}^{N-1} e^{\frac{2\pi i}{N}j(k-k')}$

If $k = k'$ , this is clearly N. Otherwise, we can write this as

$(u^k u^{k'})^* = \sum_{j=0}^{N-1} q^j$

with

$q=e^{\frac{2\pi i}{N}(k-k')}$

If q is not equal to one, i.e. if k is not equal to k’, then, according to the usual formula for a geometric series, this is equal to

$\frac{1-q^{N}}{1-q}$

However, this is zero, because $q^N = 1$ due to the periodicity of the exponential function.

Using this orthogonal basis, we can write the formula for the discrete Fourier transform simply as the hermitian product

$X_k = \langle x, u^k \rangle$

In particular, the discrete Fourier transform can be seen as the linear transformation that maps the k-th unit vector onto the vector $(u^k)^*$ . By adding a factor $1 / \sqrt{N}$ , this can be turned into a unitary transformation, i.e. in a certain sense the discrete Fourier transform is simply a rotation. This relation can also be used to easily derive a formula for the inverse of the discrete Fourier transform. In fact, if we expand the vector x into the basis $\{u^k\}_k$ , we obtain

$x = \frac{1}{N} \sum_k \langle x, u^k \rangle u^k$

and therefore

$x_k = \langle x, e_k \rangle = \frac{1}{N} \sum_j \langle x, u^j \rangle \langle u^j, e_k \rangle = \frac{1}{N} \sum_j X_j e^{\frac{2\pi i}{N} jk}$

Fourier transforms of a periodic sequence

For what follows, let us adapt and simplify our notation a bit. First, we add a factor $1 / \sqrt{N}$ to the formula for the Fourier coefficient, so that the Fourier transform is unitary. Second, we use the symbol $\eta$ to denote the N-th root of unity, i.e.

$\eta = e^{\frac{2\pi i }{N}}$

With this notation, the formula for the Fourier coefficient is then

$X_k = \frac{1}{\sqrt{N}} \sum_j x_j \eta^{-kj}$

and the inverse is given by

$x_k = \frac{1}{\sqrt{N}} \sum_j X_j \eta^{kj}$

Let us now study a special case that is highly relevant for the applications to the factoring of large numbers – the Fourier transform of a periodic sequence. Thus, suppose there is a sequence x_k and a number r called the period such that

$x_{rs + t} = x_t$

for all values of s and t that lead to valid indices. Thus, roughly speaking, after r indices, the values of the sequence repeat themselves. It is also common to reserve the term period for the smallest number with this property. We call the number $u = \frac{N}{r}$ the frequency of the sequence.

Let us now assume that the frequency is a natural number, i.e. that the period divides N, and let us try to understand what this means for the Fourier transform. Using the periodicity, we can write the coefficients as follows.

$X_k = \frac{1}{\sqrt{N}} \sum_j x_j \eta^{-jk} = \frac{1}{\sqrt{N}} \sum_{s,t} x_{sr + t}\eta^{(-sr+t)k} = \frac{1}{\sqrt{N}} (\sum_s \eta^{-srk})(\sum_t x_t \eta^{-tk})$

where s runs from 0 to u-1. We can now write the first of the sums as follows.

$\sum_{s=0}^{u-1} \eta^{-srk} = \sum_{s=0}^{u-1} e^{-\frac{2\pi i}{u}s k}$

Now this is again a geometric series with $q = e^{-\frac{2\pi i}{u}k}$ ! We can therefore conclude as above that this is zero unless q is one, i.e. unless k is a multiple of the frequency u. Thus we have shown that if the sequence x_k is periodic with integral frequency u, then all Fourier coefficients X_k are zero for which k is not a multiple of the frequency.

In the later applications, this fact will be applied in a situation where we know that a sequence is periodic, but the period is unknown. We will then perform a Fourier transformation and inspect the coefficients X_k. We can then conclude that the unknown frequency u must be a common divisor of all those indices k for which X_k is different from zero. This is exactly true if the period divides N, and we will see later that in important cases, it is still approximately true if the period does not divide N.

A quantum algorithm to compute the discrete Fourier transform

Let us now carry over our considerations to the world of quantum computing. In a quantum computer with n qubits, the Hilbert space of states is N-dimensional with N=2ⁿ, and is spanned by the basis $|k \rangle$ . Every vector can be described by the sequence of its coefficients when expanding it into this basis. Consequently, the discrete Fourier transform defines a unitary transformation on the Hilbert by applying the mapping

$\sum_k x_k |k \rangle \mapsto \sum_k X_k |k \rangle$

Now this is a unitary transformation, and as any such transformation, can be implemented by a quantum circuit. We will not go into details on this, see for instance [1], section 7.8 or section 5.1 of [2] (but be careful, these authors use a different sign convention for the Fourier transform). The important part, however, is that a quantum Fourier transform for N=2ⁿ can be realized with O(n²) quantum gates.

In contrast to this, the best known classical algorithms for computing the discrete Fourier transform are commonly known as fast Fourier transform and require O(Nn) steps. Thus it seems that we have again found a quantum algorithm which is substantially faster than its classical counterpart.

Unfortunately, this is not really true, as we have not yet defined our measurement procedure. In fact, if we measure the result of applying a quantum Fourier transform, we destroy the superposition. In addition, the coefficients in which we are interested are the amplitudes of the possible outcomes, and there is no obvious way to measure them – even if we perform the transformation several times and measure over and over again, we only obtain approximations to the probabilities which are the absolute values of the squared amplitudes, so we do not obtain the phase information. Therefore, it is far from clear whether a quantum algorithm can help to compute the Fourier transform more efficiently than it is possible with a classical algorithm.

However, most applications of the Fourier transform in quantum algorithms are indirect, using the transform as a sort of amplification step to focus amplitudes on interesting states. In the next post, we will look at Shor’s algorithm with exploits the periodicity properties of the Fourier transform to factor large composite numbers.

References

1. E. Rieffel, W. Polak, Quantum computing: a gentle introduction, MIT Press
2. M.A. Nielsen, I.L. Chuang, Quantum computation and quantum information, Cambridge University Press

Interrupts – the heartbeat of a Unix kernel

Modern operating systems are mostly event driven – network cards receive packets, users hit keys or a mouse buttons, built-in timer create events or data arrives from a hard drive. To be able to process these events, a CPU needs a mechanism to stop whatever it is currently doing and run some code designed to deal with the event – and this is what is called an interrupt.

How do interrupts work?

Formally speaking, we could define an interrupt as an event that instructs the CPU to stop the current flow of processing, jump to a defined location in memory, execute the instructions there and later, when that stream of instructions is complete, resume processing at the point where it left of.

To understand how this works, let us briefly recall some basic concepts in CPU design. First, remember that a CPU has – apart from other units – a certain set of registers, i.e. a set of easily accessible, but small pieces of memory that the CPU uses to store intermediate results of a calculation. To be a bit more specific, let us assume that we talk about an x86 CPU in protected mode. Then there are registers called EAX, EBC, ECD and EDX (and many others) that can hold 4 bytes, i.e. 32 bits, each. Instructions like the ADD command can refer to these register and, for instance, add the content of two registers and store the result in a third register.

In addition to these general purpose registers, there are a few other special registers. One of them is the register called EIP which is the instruction pointer – it points to the memory location where the instruction just executed is stored. And there is the stack pointer ESP, which points to the bottom of the stack, i.e. to an area of memory which a program can use to temporarily store data. When a program pushes data on the stack, the stack pointer is decremented, i.e. the stack grows downwards, and the data it is written to the memory location to which the stack pointer then refers. If a program pops data from the stack, the data is taken from the memory location to which the stack pointer currently refers, and the stack pointer is incremented again.

When instructions are executed one by one, the instruction pointer is simply increased after the processing of one instruction has been completed to point to the next instruction. However, when a program uses the CALL instruction to call a subroutine, the CPU will have to continue execution not at the next instruction, but at the start of the subroutine. When the subroutine completes, however, it needs to resume processing at the next instruction after the CALL instruction. So it has to save this address – called the return address – somewhere.

As there is only a small set of registers available and we might want to do nested calls, the CPU cannot use a register for this purpose, so it uses the stack. Thus, if we call a subroutine, the return address is pushed onto the stack. When the subroutine has completed, a special instruction called RET is placed in the code. This instruction tells the CPU to get the return address from the stack and resume execution at this point.

By now, you might be asking yourself why I am telling you all this. The answer is simple – interrupts work in a very similar way. In fact, when an interrupt is raised (we will see further below what this actually means), the CPU places the current value of the EIP register on the stack. It then jumps to a predefined point in memory and processes the instructions there, called the interrupt service handler (ISR). Once the ISR completes, it needs to execute a command called IRET. This command will instruct the CPU to take the stored value of EIP from the stack and reload it. Thus, the CPU will resume execution of the current program after the instruction during which the interrupt was generated.

This simple description glossed over a few details. First, interrupts are numbered, i.e. there is not only one interrupt, but in fact there are 256 so-called interrupt vectors. When an interrupt is raised, the CPU uses the interrupt vector to look up the address of the interrupt service handler in a table called the interrupt descriptor table (IDT). Thus an operating system needs to set up interrupt service handlers for all these 256 possible vectors and populate the IDT accordingly.

Second, the CPU does not only store the value of EIP on the stack, but some additional information like an error code. If you are interested in the details, you can find a description of the precise stack layout in the ctOS documentation.

And finally, an interrupt might in addition cause a change of privileges – we will learn more about this when we discuss the protected mode in one of the future posts.

Note that the CPU does not automatically place all other registers like EAX on the stack, so the interrupt service handler needs to make sure that these registers are restored to their original state before the ISR returns, otherwise the running program will continue execution with a corrupted register set (but an operating system can use this to on purpose change the values of the registers of a running program).

Sources of interrupts and interrupt routing

Now where do interrupts really come from? Basically, there are three sources of interrupts.

First, there are hardware interrupts. These are interrupts that are caused by hardware external to the CPU. An example could be a keyboard that uses an interrupt to signal that the user has pressed a key, or a timer that is programmed to generate specific interrupts periodically. We will see below how these interrupts are used in an operating system kernel.

Second, there are software interrupts. These can be exceptions or faults, i.e. interrupts that are raised by the CPU to signal some sort of error condition, like the attempt to divide by zero or a general protection fault. But software interrupts can also be raised by a program on purpose using the INT instruction.

The exact mechanism how a hardware interrupt travels from a peripheral device to the CPU is one of the most complicated and bloated areas of the PC architecture. In most cases, there is an additional piece of hardware sitting between a device and the CPU that is responsible for handling this communication and is called the interrupt controller. The first IBM compatible PCs had an interrupt controller called the PIC that was able to handle eight different hardware interrupts. However, with an increasing number of devices, this soon turned out to be not sufficient, so a second interrupt controller was cascaded with the first one to be able to manage sixteen interrupts. This itself was made a bit more complicated than it sounds by the fact that at this time, two bus systems were around – the new PCI bus and the old ISA bus – and that the interrupt routing could be programmed by the BIOS using the so-called programmable interrupt router (PIR). So we already had a bit of a complex setup, as indicated in the diagram below.

Then the first PCs started to have more than one CPU, and a more flexible mechanism was invented – the APIC. Unfortunately, the old interrupt controller was still around and could be used, making for a very complex configuration mechanism. And finally, newer devices use a mechanism called MSI that avoids an interrupt controller almost completely. If you want to read up the full story, again the ctOS documentation has all the nitty-gritty details.

Where are interrupts used?

I started this post with the bold claim that interrupts are the heartbeat of a modern operating system kernel – so let me try to justify this statement.

First, let us think about how a CPU would typically communicate with the hardware. Take a very simple example – user input. Of course, in a dialogue driven programming style, things are simple. You would print something to the screen and then wait for user input. More specifically, you would periodically, maybe within every few microseconds, ask the keyboard controller for any new data that has arrived.

Such a design is simple, but has a major disadvantage: while you are actively waiting (polling in the language of computer scientists) for input, you consume CPU time and the CPU cannot do anything else. This is not a major problem for a home computer operating system of the early eighties, but turns into a problem when you want to support multi-tasking or even multi-user capabilities.

Interrupts offer a way out. Instead of sitting in a loop and polling for new data every few thousand iterations, the CPU can hand over control to another task which is currently not expecting user input and can let the keyboard controller fire an interrupt if the user presses (or releases) a key. The interrupt service handler can then inspect the input and either put it into a buffer for later processing or initiate a task switch back to the program waiting for the input (we will look in more detail into the exact mechanics of a task switch in a later post).

A similar mechanism can be used for other input/output related processing. If, for instance, we want to read data from the hard disk, we can apply a procedure called direct memory access (DMA). With DMA, the CPU would ask the hard disk controller to load one or more sectors from the disk and then continue to work on other tasks. The controller would – in the background – read the data from the disk and transfer it into a designated area of the systems main memory. Once the transfer is complete, it would inform the CPU by raising an interrupt. The CPU could then, again in an interrupt service handler, get the data and process it further. Similar mechanism apply for networking – incoming packets can trigger interrupts, or an interrupt could signal to the CPU that the network controller is ready to send out data.

But interrupts are not only useful for I/O related tasks – they are also a major ingredient for the implementation of multi-tasking. In fact, the very first multi-tasking systems used for home PCs where based on a design called cooperative multi-tasking. With that design, a task would actively return control to the operating system after executing some time to allow other processes to run. You might want to compare this to a group of people on a hot summer day sharing a bottle of water. When everybody cooperates and passes on the bottle after a few sips, this works fine. But things go wrong if someone – for whatever reasons – just keeps on drinking until the bottle is empty. Translated back to the world of operating systems, this design allows a single process to consume the entire CPU time, so that no other process can execute any more, for instance because it is stuck in an infinite loop due to a programming error – the machine will appear to hang. Those of you who have still seens Windows 3.11 that uses this design know what I am talking about.

A more advanced design can be realized using interrupts. A modern PC does for instance have a timer that creates interrupts at a defined frequency, say 1000 Hz, i.e. one interrupt every millisecond. If the interrupt service routine triggered by the timer is performing a task switch, it is made sure that even if a process hangs, control will be returned to the operating system and potentially to a different process after at most one millisecond. This design is called preemptive multitasking because the task switch is not actively initiated by the currently running process, but the process is interrupted (preeempted) by the ISR and the operating system.

And there are even more applications that are worth being mentioned – you can use interrupts for debugging, several CPU cores can use special interrupts to communicate with each other and a thermal sensor can use an interrupt to let the CPU know that a certain temperature has been exceeded. In fact, in an operating system kernel, a lot of processing is done in an interrupt service handler, like dealing with hardware interrupts, scheduling a new task and handling signals – see the overview of the interrupt processing in ctOS below to get an idea.

There is one more point that we have ignored so far – interrupts can be used to switch back between kernel space and user space, or between ring 3 and ring 0 of a CPU. However, explaining this requires a basic understanding of the protected mode, so we will leave this for a later post.

Grover’s algorithm – unstructured search with a quantum computer

In the last post, we have looked at the Deutsch-Jozsa algorithm that is considered to be the first example of a quantum algorithm that is structurally more efficient than any classical algorithm can probably be. However, the problem solved by the algorithm is rather special. This does, of course, raise the question whether a similar speed-up can be achieved for problems that are more relevant to practical applications.

In this post, we will discuss an algorithm of this type – Grover’s algorithm. Even though the speed-up provided by this algorithm is rather limited (which is of a certain theoretical interest in its own right), the algorithm is interesting due to its very general nature. Roughly speaking, the algorithm is concerned with an unstructured search. We are given a set of N = 2ⁿ elements, labeled by the numbers 0 to 2^n-1, exactly one of which having a property denoted by P. We can model this property as a binary valued function P on the set $\{0,N-1\}$ that is zero on all but one elements. The task is to locate the element x₀ for which P(x₀) is true.

Grover’s algorithm

Grover’s algorithm presented in [1] proceeds as follows to locate this element. First, we again apply the Hadamard-Walsh operator W to the state $|0 \rangle$ of an n-qubit system to obtain a superposition of all basis states. Then, we iteratively apply the following sequence of operations.

Apply a conditional phase shift S, i.e. apply the unique unitary transformation that maps $|x \rangle$ to $(-1)^{f(x)} |x \rangle$ .
Apply the unitary transformation D called diffusion that we will describe below

Finally, after a defined number of outcomes, we perform a measurement which will collaps the system into one of the states $|x \rangle$ . We claim – and will see why this is true below – that for the right number of iterations, this value x will, with a high likelihood, be the solution to our problem, i.e. equal to x₀.

Before we can proceed, we need to define the matrix D. This matrix is $\frac{2}{N} - 1$ along the diagonal, with N = 2ⁿ, and $\frac{2}{N}$ away from the diagonal. In terms of basis vectors, the mapping is given by

$|i \rangle \mapsto \frac{2}{N} (\sum_j |j \rangle) - |i \rangle$

Consequently, we see that

$D \sum_i a_i |i \rangle = \sum_i (2 \bar{a} - a_i) |i \rangle$

where $\bar{a}$ is the average across the amplitudes $a_i$ . Thus geometrically, the operation D performs an inversion around the average. Grover shows that this operation can be written as minus a Hadamard-Walsh operation followed by the operation that flips the sign for $|0 \rangle$ , followed by a second Hadamard-Walsh transformation.

For the sake of completeness, let us also briefly discuss the first transformation employed by the algorithm, the conditional phase shift. We have already seen a similar transformation while studying the Deutsch-Jozsa algorithm. In fact, we have shown in the respective blog post that the circuit displayed below (with the notation slightly changed)

performs the required operation

$|\psi \rangle = \sum_x a_x |x \rangle \mapsto |\psi' \rangle = \sum_x a_x (-1)^{P(x)} |x \rangle$

Let us now see how why Grover’s algorithm works. Instead of going through the careful analysis in [1], we will use bar charts to visualize the quantum states (exploiting that all involved matrices are actually real valued).

It is not difficult to simulate the transformation in a simple Python notebook, at least for small values of N. This script performs several iterations of the algorithm and prints the result. The diagrams below show the outcome of this test.

Let us go through the diagrams one by one. The first diagram shows the initial state of the algorithm. I have used 3 qubits, i.e. n = 3 and N = 8. The initial state, after applying the Hadamard-Walsh transform to the zero state, is displayed in the first line. As expected, all amplitudes are equal to 1 over the square root of eight, which is approximately 0.35, i.e. we have a balanced superposition of all states.

We now apply one iteration of the algorithm. First, we apply the conditional phase flip. The element we are looking for is in this case located at x = 2. Thus, the phase flip will leave all basis vectors unchanged except for $|2 \rangle$ and it will change the amplitude of this vector to – 0.35. This will change the average amplitude to a value slightly below 0.35. If we now perform the inversion around the average, the amplitudes of all basis vectors different from $|2 \rangle$ will actually decrease, whereas the amplitude of $|2 \rangle$ will increase. The result is displayed in the second line of the diagram.

Thus, what really happens in this case is an amplitude amplification – we increase the amplitude of one component of the superposition while decreasing all the others.

The next few lines show the result of repeating these two steps. We see that after the second iteration, almost all of the amplitude is concentrated on the vector $|2 \rangle$ , which represents the solution we are looking for. If we now perform a measurement, the result will be 2 with a very high probability!

It is interesting to see that when we perform one more iteration, the difference between the amplitude of the solution and the amplitudes of all other components decreases again. Thus the correct choice for the number of iterations is critical to make the algorithm work. In the last line, we have plotted the difference between the amplitude of $|2 \rangle$ and the other amplitudes (more precisely, the ratio between the amplitude of $|2 \rangle$ and the second largest amplitude) on the y-axis for the different number of iterations on the x-axis. We see that the optimal number of iterations is significantly below 10 (actually five iterations give the best result in this case), and more iterations decrease the likelihood of getting the correct result out of the measurement again. In fact, a careful analysis carried out in [2] shows that for large values of N, the best number of iterations is given by $\frac{\pi}{4} \sqrt{N}$ , and that doubling the number of iterations does in general lead to a less optimal result.

Generalizations and amplitude amplification

In a later paper ([3]), Grover describes a more general setup which is helpful to understand the basic reason why the algorithm works – the amplitude amplification. In this paper, Grover argues that given any unitary transformation U and a target state (in our case, the state representing the solution to the search problem), the probability to meet the target state by applying U to a given initial state can be amplified by a sequence of operations very much to the one considered above. We will not go into details, but present a graphical representation of the algorithm.

So suppose that we are given an n-qubit quantum system and two basis vectors – the vector t representing the target state and an initial state s. In addition, assume we are given a unitary transformation U. The goal is to reach t from s by subsequently applying U itself and a small number of additional gates.

Grover considers the two-dimensional subspace spanned by the vectors s and U^-1t. If, within this subspace, we ever manage to reach U^-1t, then of course one more application of U will move us into the desired target state.

Now let us consider the transformation

$Q = - I_s U^{-1} I_t U$

where I_x denotes a conditional phase shift that flips the phase on the vector $|x \rangle$ . Grover shows that this transformation does in fact leave our two-dimensional subspace invariant, as indicated in the diagram below.

He then proceeds to show that for sufficiently small values of the matrix element U_ts, the action of Q on this subspace can approximately be described as a rotation by the angle $\frac{2}{|U_{ts}|}$ . Applying the operation Q n times will then approximately result in a superposition of the form

$\cos (\frac{2n}{|U_{ts}|})|s \rangle + a U^{-1}|t \rangle$

Thus if we can make the first coefficient very small, i.e. if $\frac{4n}{|U_{ts}|}$ is close to a multiple of $\pi$ , then one application of U will take our state to a state very close to t.

Let us link this description to the version of the Grover algorithm discussed above. In this version, the initial state s is the state $|0 \rangle$ . The transformation U is the Hadamard-Walsh transformation W. The target state is $|x_0 \rangle$ where x₀ is the solution to the search problem. Thus the operation I_t is the conditional phase shift that we have denoted by S earlier. In addition, Grover shows in [1] already that the diffusion operator D can be expressed as -W I₀ W. Now suppose we apply the transformation Q n times to the initial state and then apply U = W once more. Then our state will be

$W Q \dots Q |0 \rangle$

This can be written as

$W (-I_0 W S W) (-I_0 W S W) \dots (-I_0 W S W) |0 \rangle$

Regrouping this and using the relation D = -W I₀ W, we see that this is the same as

$- (W I_0 W) S (- W I_0 W) S \dots \dots (- W I_0 W) S W |0 \rangle = D S \dots D S W |0 \rangle$

Thus the algorithm can equally well be described as applying W once to obtain a balanced superposition and then applying the sequence DS n times, which is the formulation of the algorithm used above. As $|U_{ts} | = \frac{1}{\sqrt{N}}$ in this case, we also recover the result that the optimal number of iterations is $\frac{\pi}{4} \sqrt{N}$ for large N.

Applications

Grover’s algorithm is highly relevant for theoretical reasons – it applies to a very generic problem and (see the discussions in [1] and [2]) is optimal, in the sense that it provides a quadratic speedup compared to the best classical algorithm that requires O(N) operations, and that this cannot be improved further. Thus Grover’s algorithm provides an interesting example for a problem where a quantum algorithm delivers a significant speedup, but no exponential speedup as we will see it later for Shor’s algorithm.

However, as discussed in detail in section 9.6 of [4], the relevance of the algorithm for practical applications is limited. First, the algorithm applies to an unstructured search, i.e. a search over unstructured data. In most practical applications, we deal with databases that have some sort of structure, and then more efficient search algorithms are known. Second, we have seen that the algorithm requires $O(\sqrt{N})$ applications of the transformation U_P. Whether this is better than the classical algorithm does of course depend on the efficiency with which we can implement this with quantum gates. If applying U_P requires O(N) operations, the advantage of the algorithm is lost. Thus the algorithm only provides a significant speedup if the operation U_P can be implemented efficiently and there is no additional structure that a classical algorithm could exploit.

Examples of such problems are brute forces searches as they appear in some crypto-systems. Suppose for instance we are trying to break a message that is encrypted with a symmetric key K, and suppose that we know the first few characters of the original text. We could then try to use an unstructured search over the space of all keys to find a key which matches at least the few characters that we know.

In [5], a more detailed analysis of the complexity in terms of qubits and gates that a quantum computer would have to attack AES-256 is made, arriving at a size of a few thousand logical quantum bits. Given the current ambition level, this does not appear to be completely out of reach. It does, however, not render AES completely unsecure. In fact, as Grover’s algorithm essentially results in a quadratic speedup, a code with a key length of n bits in a pre-quantum world is essentially as secure as the same code with a key length of 2n in a post-quantum world, i.e. roughly speaking, doubling the key length compensates the advantage of quantum computing in this case. This is the reason why the NIST report on post-quantum cryptography still classifies AES as inherently secure assuming increased key sizes.

In addition, the feasibility of a quantum algorithm is not only determined by the number of qubits required, but also by other factors like the depth, i.e. the number of operations required, and the number of quantum gates – and for AES, the estimates in [5] are significant, for instance a depth of more than 2¹⁴⁵ for AES-256, which is roughly 10⁴³. Even if we assume a switching time of only 10^-12 seconds, we still would require astronomical 10³¹ seconds, i.e. in the order of 10²³ years, to run the algorithm.

Even a much less sophisticated analysis nicely demonstrates the problem behind these numbers – the number of iterations required. Suppose we are dealing with a key length of n bits. Then we know that the algorithm requires

$\frac{\pi}{4} \sqrt{2^n} \approx 0.8 \sqrt{2}^n$

iterations. Taking the decimal logarithm, we see that this is in the order of 10^0.15*n. Thus, for n = 256, we need in the order of 10³⁸ iterations – a number that makes it obvious that AES-256 can still be considered secure for all practical purposes.

So overall, there is no reason to be overly concerned about serious attacks to AES with sufficiently large keys in the near future. For asymmetric keys, however, we will soon see that the situation is completely different – algorithms like RSA or Elliptic curve cryptography are once and for all broken as soon as large-scale usable quantum computer become reality. This is a consequence of Shor’s algorithm that we will study soon. But first, we need some more preliminaries that we will discuss in the next post, namely quantum Fourier transforms.

References

1. L.K. Grover, A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing (STOC), May 1996, pages 212-219, available as arXiv:quant-ph/9605043v3
[2] M. Boyer, G. Brassard, P. Høyer, A. Tapp, Tight bounds on quantum searching, arXiv:quant-ph/9605034
3. L.K. Grover, A framework for fast quantum mechanical algorithms, arXiv:quant-ph/9711043
4. E. Rieffel, W. Polak, Quantum computing – a gentle introduction, MIT Press
5. M. Grassl, B. Langenberg, M. Roetteler, R. Steinwandt, Applying Grover’s algorithm to AES: quantum resource estimates, arXiv:1512.04965

Get your kernel going – the boot process

Most careers in operating system development probably start with a seemingly simple task – produce a program that, at start time, takes full control of a computer and prepares for the execution of the actual operating system, i.e. boot the computer. It turns out, however, that – thanks to the complexity of modern x86 based hardware – this is easier said than done. In this post, we will look at the boot process in a bit more detail.

History of the boot process

To understand the boot process in a modern PC, it is actually useful to go back into the past a bit. The first home computer that I owned was an Amstrad CPC 464 with a Zilog Z80 CPU. Like any other CPU I am aware of, this CPU stores the memory location of the next instruction to be executed in a register, called – in this case – the program counter (PC). When you turn on that machine, the CPU is in its initial state, with the value of the PC being equal to its initial value 0x0000. Now, at this point in memory space, there was actually no RAM, but a ROM that contained the CPC firmware. Starting at address 0x0000, the so-called restart block was located which then took over and initialized the system. And let the fun begin …(picture taken on the fabulous CPCBox, a browser-based CPC emulator).

This mechanism is straightforward and fast – when you turn on the machine, the operating system is available immediately and you can start to work with it. However, there are obvious disadvantages, the most important one being that updates are difficult once a machine is shipped, and even late in the manufacturing process.

The developers of the famous IBM PC XT decided to use a different approach. Instead of loading the full operating system from ROM, the ROM did only contain a firmware called the BIOS, a small set of routines needed for some basic operations, like reading from the hard drive or a disk, and a short startup routine. When the system comes up, the CPU again starts execution at some predefined point in memory, where the BIOS startup routine is located. This routine would then typically execute some self-tests and then load the actual operating system from the hard drive or a floppy disk.

Loading the operating system does actually happen in two phases. In the first phase, the BIOS loads the so-called boot loader. The boot loader is located at a fixed location of the hard drive, specifically in the first sector (called the master boot record (MBR)), and occupies a bit less than 512 bytes. This boot loader is brought into memory and then executed. It is then responsible for locating the actual operating system and loading it.

So far, this is comparatively simple. Unfortunately, PC hardware then started to evolve, and with every step in the evolution, the boot process had to be adapted so that it could make use of new features, but still be backwards compatible. For instance, when the x86 CPU was enhanced by adding the so-called protected mode in 1985, the BIOS would still operate in the older real mode to stay compatible with legacy operating systems. When an operating system wanted to make use of the new features of the protected mode, either the boot loader or the early stages of the operating system kernel had to switch the CPU into protected mode. However, as the BIOS is still 16 bit code, its routines can no longer be accessed once that switch has been completed, in particular reading from a hard drive is no longer easily possible until the initialization of the operating system has reached a certain point. This makes for interesting chicken-and-egg problems: if the operating system that needs to be loaded exceeds a certain size, you will have to switch to protected mode to be able to utilize the full memory, but once this is done it becomes much more complicated to access the hard drive to load the operating system files.

To solve this, several sophisticated boot mechanisms were implemented by various boot loaders. One approach was to actually compress the operating system image so that it could be loaded into memory once the BIOS was still accessible, then perform the switch to protected mode and then decompress the image. Another approach is to boot the system in several stages. The boot code for stage 0 would, for instance, be stored in the MBR, which would then load a stage 1. This stage 1 would contain sufficient functionality to read data from a standard file system, including a hard disk driver. It would then switch to protected mode and use this functionality to load the stage 2, which would then start the actual operating system. The GRUB bootloader, for instance, uses a similar (but slightly different) mechanism.

Booting a modern PC

Roughly around 2005, the industry started to introduce the UEFI as the next generation standardized PC firmware, aiming to become the successor of the outdated BIOS. The UEFI is much more powerful than the BIOS. Instead of loading one sector from a specified location on the hard drive, the UEFI is able to read from a file system. Thus the initial operating system image can be an ordinary executable file, stored on a file system. The UEFI will search certain standard directories for files with predefined names (like BOOTX64.EFI) and execute such a file if it is found. This file then executes in an UEFI environment in 32 bit protected mode or 64 bit long mode and has access to UEFI services to perform operations like input, output or hard drive access. These services can then be used to load the operating system, before eventually control of the system is handed over to the operating system and the UEFI services must no longer be used.

However, the BIOS used to be more than just a set of routines – it also contained several configuration tables that provide basic information on the hardware relevant for the operating system, like the available graphics modes, the number and type of available CPUs, the available memory and reserved memory areas and information on the configuration of the system interrupts. This information is now presented to an operating system as part of the ACPI (Advanced configuration and power interface). The ACPI is a complex collection of tables, some of which are static, some of which are actually dynamic, i.e. contain byte code that needs to be run by a bytecode interpreter.

So far, the description has focused on the standard case for a home PC – booting from a local storage like hard drive, an USB stick or a CD-ROM. However, several methods exist to boot over a network as well. The PXE boot protocol, for example, is a mechanism to boot an operating system over a network. When PXE boot is used, either a boot loader or a sufficiently modern BIOS initializes the clients network card and establishes a connection to server. The server runs a TFTP server (TFTP is a simplified version of the FTP protocol) and the client uses the TFTP protocol to transfer an operating system image over the network. This is the technology behind thin clients, i.e. clients that only contain a ROM based firmware capable of executing a PXE based boot process, but no local storage and no local copy of the operating system.

To get an idea how the full boot process looks like on a modern PC, let us take a look at the sequence of steps that are executed when my homebrew operating system ctOS starts up. Here is a screenshot of the system once the startup sequence is completed (taken using the QEMU emulator).

The most important steps that actually execute in the background and produce this output are as follows.

The hardware (or the emulator) loads the BIOS (SeaBIOS in this case)
The BIOS locates the boot loader (GRUB2 in my case) on the hard drive and loads it in several stages
GRUB2 starts to execute on the first CPU in the system, called the bootstrap CPU
When GRUB2 hands over control to the operating system, the system is already in protected mode, however certain system tables are in a preliminary or incomplete state. Thus these tables are initialized first
Then all components of the kernel are initialized. This includes device drivers, interrupts, the memory manager, the process manager and the TCP/IP stack.

During this stage, the system will also read the BIOS or ACPI configuration tables and detect and initialize other hardware components like the interrupt controller, the system clock, the keyboard, or attached PCI devices like hard drives and network cards

Next, all the other CPUs in the system are initialized and put into protected mode
Finally, the root process is started and the command line interface is located on the disk and started – at this point the boot process is complete and the user takes over control of the system

Of course for a more advanced operating system, the actual boot process would do much more – loading a graphical user interface, for instance, or starting system daemons. However, technically, once we get to the point that a user space program can execute, most of the low level subtleties are mastered and we can work in a stable environment.

This concludes our discussion of the boot process. With the next post in this series, I will start our trip through the various components of an operating system. Happy booting!