Ultimately, VertexAI is about the processing of data. In previous posts in this series, we have placed our data in a GCS bucket and referenced it within our pipelines directly by the URI – you could call this a self-managed dataset. Alternatively, VertexAI also allows you to defined managed datasets which are stored in a…More
The nuts and bolts of VertexAI – networking
When we access a VertexAI predicition endpoint, we usually do this using the Google API endpoint, i.e. we access a public IP address. For some applications, it is helpful to be able to connect to a prediction endpoint via a private IP address from within a VPC. Today, we will see how this works and…More
The nuts and bolts of VertexAI – pipeline metadata
When you assemble and run a custom job, the Vertex AI platform is not aware of the inputs that you consume and the outputs that you create in this job, and consequently, it is up to you to create execution and artifact metadata and the corresponding relations between executions, input artifacts and output artifacts. For…More
The nuts and bolts of VertexAI – pipelines under the hood
In our previous post, we have covered the process of creating pipeline components, defining a pipeline and running the pipeline in Vertex AI. However, parts of this appeared to be a bit mysterious. Today, we will take a closer look at what is going on behind the scenes when we create and run a pipeline…More
The nuts and bolts of Vertex AI – introduction to pipelines
So far, we have worked with individual jobs. However, a typical machine learning flow is more complicated than this – you might have to import data, transform it, run a training, validate the outcomes or do a hyperparameter search, package a model and deploy it. Instead of putting all this into a single job, VertexAI…More
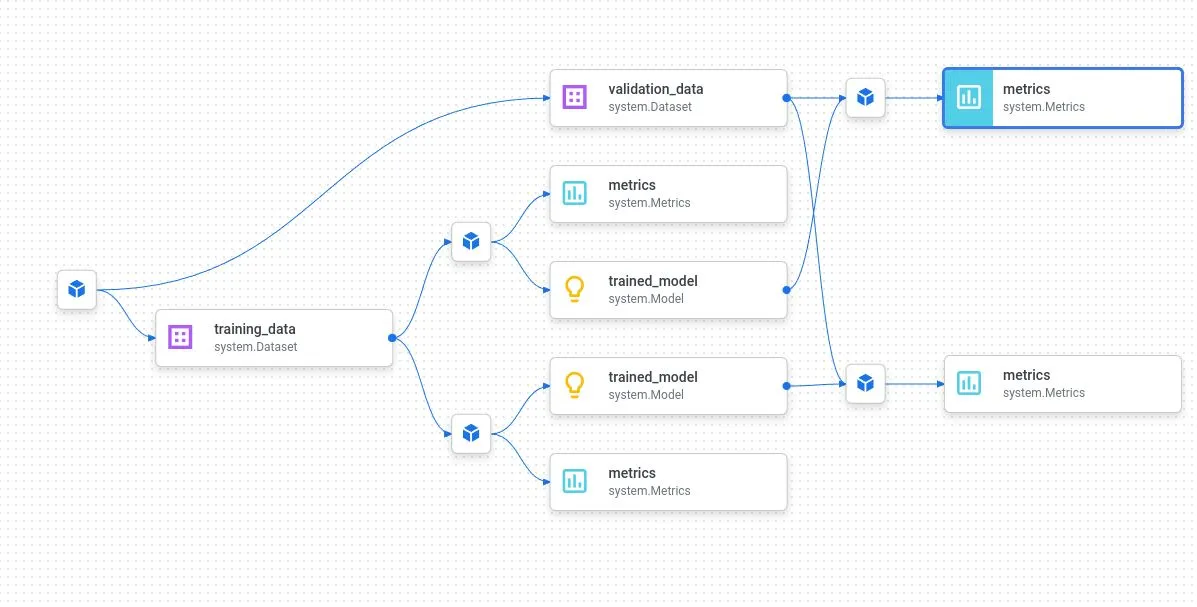
The nuts and bolts of VertexAI – metadata, logging and metrics
One of the core functionalities of every machine learning platform is traceability – we want to be able to track artifacts like models, training jobs and input data and tie all this together so that given a model version, we can go back all the way to the training data that we have used to…More
The nuts and bolts of VertexAI – custom training jobs
In the previous post, we have seen how to store trained models and how to spin up prediction endpoints. Now we will follow the ML lifecycle backwards and talk about how you actually train models on the platform. There are several options to do this and we start with the most basic one – custom…More
The nuts and bolts of VertexAI – prediction endpoints and model versions
In the last post, we have learned how to package a model and upload it into the model registry. Today, we will see how we can deploy a model from the registry to an endpoint and use that endpoint to make predictions. We will also learn how a model can be exported again and how…More
The nuts and bolts of VertexAI – models and model archives
Having completed our setup in the previous post, we will now dive into models. We will learn how a model is packaged and how we can upload models into the VertexAI model registry for later use, for instance in a pipeline job. Overview Before we dive into the details, let us first try to understand…More
The nuts and bolts of VertexAI – overview
Today, all major cloud providers have established impressive machine learning capabilities on their respective platforms – Amazon has AWS SageMaker, Google has VertexAI and Microsoft has Azure Machine Learning. Being tired of spinning up and shutting down GPU-enabled virtual machines manually, I started to explore one of them a couple of months ago – Googles…More