Category Archives: Machine learning

Mastering large language models – Part XVI: instruction fine-tuning and FLAN-T5

In most of our previous posts, we have discussed and used transformer networks that have been trained on a large set of data using teacher forcing. These models are good at completing a sentence with the most likely next token, but are not optimized for following instructions. Today, we will look at a specific family of networks that have been trained to tailor their response according to instructions – FLAN-T5 by Google.

If you ask a language model that has been trained on a large data set to complete a prompt that represents an instruction or a question, the result you will obtain is the most likely completion of the prompt. This, however, might not be the answer to your question – it could as well be another question or another instruction, as the model is simply trying to complete your prompt. For many applications, this is clearly not what we want.

One way around this is few-shot learning which basically means that you embed your instruction into a prompt that somehow resembles the first few lines of a document so that the answer that you expect is the most natural completion, giving the model a chance to solve your task by doing what it can do best, i.e. finding completions. This, however, is not really a satisfying approach and you might ask whether there is a way to fix the problem at training time, not at inference time. And in fact there is a method to train a model to recognize and follow instructions – instruction fine-tuning.

Most prominent models out there like GPT did undergo instruction fine tuning at some point. Today we will focus on a model series called FLAN-T5 which has been developed by Google and for which the exact details of the training process have been published in several papers (see the references). In addition, versions of the model without instruction fine tuning are available so that we can compare them with the fine-tuned versions.

In [1], instruction fine-tuning has been applied to LaMDA-PT, a decoder-only transformer model that Google had developed and trained earlier. In [2], the same method has been applied to T5, a second model series presented first in [3]. The resulting model series is known as FLAN-T5 and available on the Hugginface hub. So in this post, we will first discuss T5 and how it was trained and than explain the instruction fine tuning that turned T5 into FLAN-T5.

T5 – an encoder-decoder model

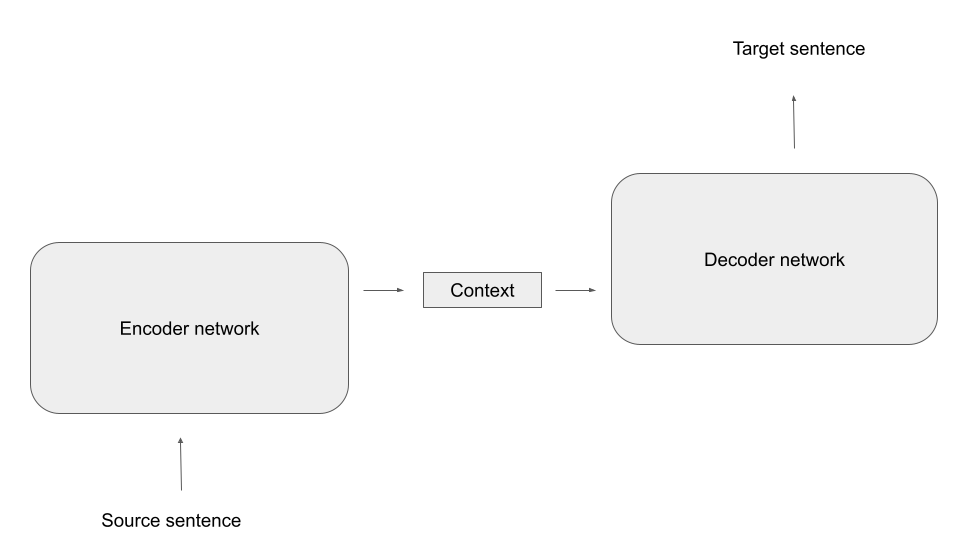
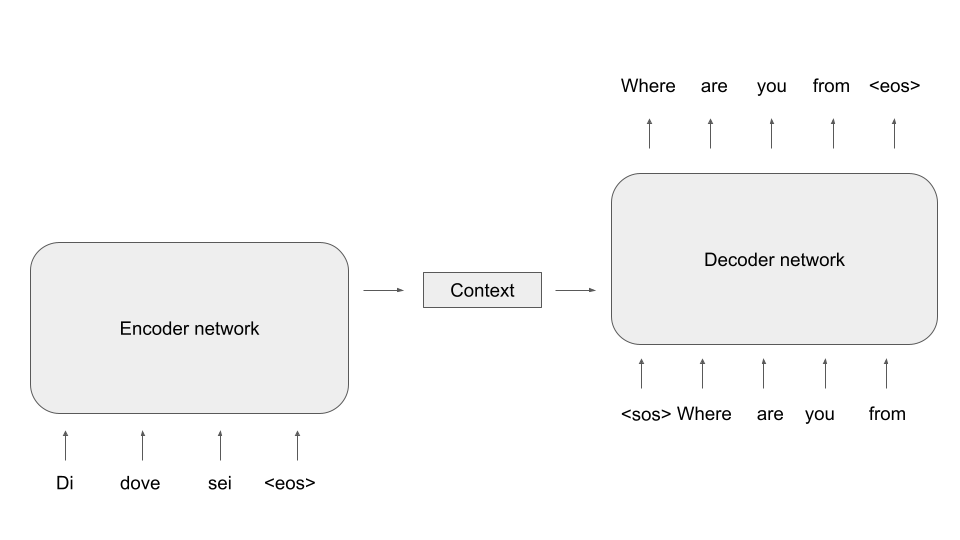
Other than most of the models we have played with so far, T5 is a full encoder-decoder model. If you have read my previous post on transformer blocks and encoder-decoder architectures, you might remember the following high-level overview of such an architecture.

For pre-training, Google did apply a method known as masking. This works as follows. Suppose your training data contains the following sentence:

The weather report predicted heavy rain for today

If we encode this using the the encoder used for training T5, we obtain the sequence of token

[37, 1969, 934, 15439, 2437, 3412, 21, 469, 1]

Note that the last token (with ID 1) is the end-of-sentence token that the tokenizer will append automatically to our input. We then select a few token in the sentence randomly and replace each of them with one of 100 special token called extra_id_NN, where NN is a number between 0 and 99. These token have IDs ranging from 32000 to 32099, where 32099 is extra token 0 and 32000 is extra token 99. After applying this procedure known as masking our sentence could look as follows

The weather report predicted heavy <extra_id_0> for today

or

[37, 1969, 934, 15439, 2437, 32099, 21, 469, 1]

We now train the decoder to output a list of the extra token used, followed by the masked word. So in our case, the target sequence for the decoder would be

<extra_id_0> rain

or, again including the end-of-sentence token

[32099, 3412, 1]

In other words, we ask our model to guess the word that has been replaced by the mask (this will remind you of the word2vec algorithm that I have presented in a previous post). To train the combination of encoder and decoder to reach that objective, we can again apply teacher forcing. For that purpose, we shift the labels to the right by one and append a special token called the decoder start token to the left (which, by the way, is identical to the padding token 0 in this case). So the input to the decoder is

[0, 32099, 3412]

We then can calculate the cross-entropy loss between the decoder output and the labels above and apply gradient descent as usual. I have put together a notebook for this post that walks you through an example and that you can also run on Google Colab as usual.

Pre-training using masking was the first stage in training T5. In a second stage, the model was fine-tuned on a set of downstream tasks. Examples for these tasks include translation, summarization, question answering and reasoning. For each task, the folks at Google defined a special format in which the model received the inputs and in which the output was expected. For translation, for instance, the task started with

“translate English to German: “

followed by the sentence to be translated, and the model was trained to reply with the correct translation. Another example is MNLI, which is a set of pairs of premise and hypothesis, and the model is supposed to answert with one word indicating whether a premise implies the hypothesis, is a contradiction to it or is neutral towards the hypothesis. In this case, the input is a sentence formatted as

“mnli premise: … premise goes here… hypothesis: … hypothesis goes here…

and the model is expected to answer with one of the three words “entailment”, “contradiction” or “neutral”. So all tasks are presented to the model as pure text and the outcome is expected to be pure text. My notebook contains a few examples of how this works.

From T5 to FLAN-T5

After the pre-training using masking and the fine-tuning, T5 is already a rather powerful model, but still is sometimes not able to deduce the correct task to perform. In the notebook for this post, I hit upon a very illustrative example. If we feed the sentence

Please answer the following question: what is the boiling temperature of water?

into the model, it will not reply with the actual boiling point of water. Instead, it will fall back to one of the tasks it has been trained on and will actually translate this to German instead of answering the question.

This is where instruction fine-tuning [2] comes into play. To teach the model to recognize instructions as such and to follow them, the T5 model was trained on a large number of additional tasks, phrased in natural language.

To obtain a larger number of tasks from the given dataset, the authors applied different templates to each task. If, for instance, we are given an MNLI task with a hypothesis H and a premise P, we could present this in several ways to the model, i.e. according to several templates. We could, for instance, turn the data point into natural language using the template

“Premise: P. Hypothesis: H. Does the premise entail the hypothesis?”

Or we could phrase this as

Based on the premise P, can we conclude that the hypothesis H is true?

By combining every data point from the used data set with a certain number of templates, a large dataset for the fine-tuning was obtained, and the model learned to deal with many different instructions referring to the same type of task, which hopefully would enable the model to infer the correct tasks for an unseen template at test time. As Google published the code to generate the data, you can take a look at the templates here.

Also note that the data contains some CoT (chain-of-thought) prompting, i.e. some of the instruction templates for reasoning tasks include phrases like “apply reasoning step-by-step” to prepare the model for later chain-of-thought prompting.

In the example in my notebook, the smallest FLAN-T5 model (i.e. T5 after this additional fine-tuning procedure) did at least recognize that the input is a question, but the reply (“a vapor”) is still not what we want. The large model does in fact reply with the correct answer (212 F).

Instruction fine-tuning has become the de-facto standard for large language models. The InstructGPT model from which ChatGPT and GPT-4 are derived, however, did undergo an additional phase of training – reinforcement learning from human feedback. This is a bit more complex, and as many posts on this exist which unfortunately do only scratch the surface I will dive deeper into this in the next post which will also conclude this series.

References

[1] J. Wei et al., Finetuned Language Models Are Zero-Shot Learners, arXiv:2109.01652
[2] H.W. Chung et al., Scaling Instruction-Finetuned Language Models, arXiv:2210.11416
[3] C. Raffel et al., Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer, arXiv:1910.10683

Mastering large language models Part XV: building a chat-bot with DialoGPT and Streamlit

Arguably, a large part of the success of models like GPT is the fact that they have been equipped with a chat frontend and proved able to have a dialogue with a user which is perceived as comparable to a dialogue you would have with another human. Today, we will see how transformer based language models can be employed for that purpose.

In the previous post, we have seen how we can easily download and run pretrained transformer models from the Huggingface hub. If you play with my notebook on this a bit, you will soon find that they do exactly what we expect them to do – find the most likely completion. If, for instance, you use the promt “Hello”, followed by the end-of-sentence token tokenizer.eos_token, they will give you a piece of text starting with “Hello”. This could be, for instance, a question that someone has posted into a Stackexchange forum.

If you want to use a large language model to build a bot that can actually have a conversation, this is usually not what you want. Instead, you want a completion that is a reply to the prompt. There are different ways to achieve this. One obvious approach that has been taken by Microsoft for their DialoGPT model is to already train the model (either from scratch or via fine-tuning) on a dataset of dialogues. In the case of DialoGPT, the dataset has been obtained by scraping from Reddit.

A text-based chat-bot

Before discussing how to use this model to implement a chat-bot, let us quickly fix a few terms. A conversation between a user and a chat-bot is structured in units called turns. A turn is a pair of a user prompt and a response from the bot. DialoGPT has been trained on a dataset of conversations, modelled as a sequence of turns. Each turn is a sequence of token, where the user prompt and the reply of the bot are separated by an end-of-sentence (EOS) token. Thus a typical (very short) dialogue with two turns could be represented as follows

Good morning!<eos>Hi<eos>How do you feel today?<eos>I feel great<eos>

Here the user first enters the prompt “Good morning!” to which the bot replies “Hi”. In the second turn, the user enters “How do you feel today” and the bot replies “I feel great”.

Now the architecture of DialoGPT is identical to that of GPT-2, so we can use what we have learned about this class of models (decoder-only models) to sample from it. However, we want the model to take the entire conversation that took place so far into account when creating a response, so we feed the entire history, represented as a sequence of token as above, into the model when creating a bot response. Assuming that we have a function generate that accepts a prompt and generates a reply until it reaches and end-of-sentence token, the pseudocode for a chat bot would therefore look as follows.

input_ids = []
while True:
    prompt = input("User:")
    input_ids.extend(tokenizer.decode(prompt))
    input_ids.append(tokenizer.eos_token)
    response = generate(input_ids)
    print(f"Bot: {tokenize.decode(response)}"
    input_ids.extend(response)

Building a terminal-based chat-bot on top of DialoGPT is now very easy. The only point that we need to keep in mind is that in practice, we will want to cache past keys and values as discussed in the last post. As we need the values again in the next turn which will again be based on the entire history, our generate function should return these values and we will have to pass them back to the function in the next turn. An implementation of generate along those lines can be found here in my repository. To run a simple text-based chatbot, simply do (you probably want to run this in a virtual Python environment):

git clone https://github.com/christianb93/MLLM
cd MLLM
pip3 install -r requirements.txt
cd chatbot
python3 chat_terminal.py

The first time you run this, the DialoGPT model will be downloaded from the hub, so this might take a few minutes. To select a different model, you can use the switch --model (use --show_models to see a list of valid values).

Using Streamlit to build a web-based chat-bot

Let us now try to build the same thing with a web-based interface. To do this, we will use Streamlit, which is a platform designed to easily create data-centered web applications in Python.

The idea behind Streamlit is rather simple. When building a web-based applicaton with Streamlit, you put together an ordinary Python script. This script contains calls into the Streamlit library that you use to define widgets. When you run the Streamlit server, it will load the Python script, execute it and render an HTML page accordingly. To see this in action, create a file called test.py in your working directory containing the following code.

import streamlit as st 


value = st.slider(label = "Entropy coefficient", 
          min_value = 0.0, 
          max_value = 1.0)
print(f"Slider value: {value}")

Then install streamlit and run the applications using

pip3 install streamlit==1.23.1 
streamlit run test.py

Now a browser window should open that displays a slider, allowing you to select a parameter between 0 and 1.

In the terminal session in which you have started the Streamlit server, you should also see a line of output telling you that the value of the slider is zero. What has happened is that Streamlit has started an HTTP server listening on port 8501, processed our script, rendered the slider that we have requested, returned its current value and then entered an internal event loop outside of the script that we have provided.

If now change the position of the slider, you will see a second line printed to the terminal containing the new value of the slider. In fact, if a user interacts with any of the widgets on the screen, Streamlit will simply run the script once more, this time returning the updated value of the slider. So behind the scenes, the server is sitting in an event loop, and whenever an event occurs, it will not – like frontend frameworks a la React will do it – use callbacks to allow the application to update specific widgets, but instead run the entire script again. I recommend to have a short look at the section “Data flow” in the Streamlit documentation which explains this in a bit more detail.

This is straightforward and good enough for many use cases, but for a chat bot, this creates a few challenges. First, we will have to create our model at some point in the script. For larger models, loading the model from disk into memory will take some time. If we do this again every time a user interacts with the frontend, our app will be extremely sluggish.

To avoid this, Streamlit supports caching of function values by annotating a function with the decorator st.cache_resource. Streamlit will then check the arguments of the function against the cached values. If the arguments match a previous call, it will directly return a reference to the cached response without actually invoking the function. Note that here a reference is returned, meaning in our case that all sessions share the same model.

The next challenge that we have is that our application requires state, for instance the chat history or the cached past keys and values, which we have to preserve for the entire session. To maintain session-state, Streamlit offers a dictionary-like object st.session_state. When we run the script for the first time, we can initialize the chat history and other state components by simply adding a respective key to the session state.

st.session_state['input_ids'] = []

For subsequent script iterations, i.e. re-renderings of the screen, that are part of the same session, the Streamlit framework will then make sure that we can access the previously stored value. Internally, Streamlit is also using the session state to store the state of widgets, like the position of a slider or the context of a text input field. When creating such a widget, we can provide the extra parameter key which allows us to specify the key under which the widget state is stored in the session state.

A third feature of Streamlit that turns out to be useful is to use conventional callback functions associated with a widget. This makes it much easier to trigger specific actions when a specific widget changes state, for instance if the user submits a prompt, instead of re-running all actions in the script every time the screen needs to be rendered. We can, for instance, define a widget that will hold the next prompt and, if the user hits “Return” to submit the prompt, invoke the model within the callback. Inside the callback function, we can also update the history stored in the session state.

def process_prompt():
    #
    # Get widget state to access current prompt
    #
    prompt = st.session_state.prompt
    #
    # Update input_ids in session state
    #
    st.session_state.input_ids.extend(tokenizer.encode(prompt))
    st.session_state.input_ids.append(tokenizer.eos_token_id)
    #
    # Invoke model
    #
    generated, past_key_values, _ = utils.generate(model = model, 
                                            tokenizer = tokenizer, 
                                            input_ids = st.session_state.input_ids, 
                                            past_key_values = st.session_state.past_key_values, 
                                            temperature = st.session_state.temperature, debug = False)
    response = tokenizer.decode(generated).replace('<|endoftext|>', '')
    #
    # Prepare next turn
    #
    st.session_state.input_ids.extend(generated)

Armed with this understanding of Streamlit, it is not difficult to put together a simple web-based chatbot using DialoGPT. Here is a screenshot of the bot in action.

You can find the code behind this here. To run this, open a terminal and type (switching to a virtual Python environment if required):

git clone https://github.com/christianb93/MLLM
cd MLLM
pip3 install -r requirements.txt
cd chatbot
streamlit run chat.py

A word of caution: by default, this will expose port 8501 on which Streamlit is listening on the local network (not only on localhost) – it is probably possible to change this somewhere in the Streamlit configuration, but I have not tried this.

Also remember that the first execution will include the model download that happens in the background (if you have not used that model before) and might therefore take some time. Enjoy your chats!

Mastering large language models – Part XIV: Huggingface transformers

In the previous post, we have completed our journey to being able to code and train a transformer-based language model from scratch. However, we have also seen that in order to obtain professional results, we need an enormous amount of resources, i.e. training data and compute power. Luckily, there are some pre-trained transformer models that we can use, be it directly for inference or as a basis for further fine-tuning. Today, we will take a look at the probably most prominent platform that exists for that purpose – the Huggingface platform.

Huggingface is a company that offers a variety of services around machine learning. In our context, we will mainly be interested in the wo of their products – the transformers library and the Huggingface hub, which is a platform to which scientists and enthusiasts can upload weights and trained models to make them available for everyone using the Huggingface transformer library.

As a starting point, let us first make sure that we have the library installed. For this post (and the entire series) I have used version 4.27.4, which you can install as usual.

pip3 install transformers==4.27.4

The recommended starting point for working with the library is a pipeline, which is essentially a container that includes everything which we typically need, most notably a tokenizer and a model. As the intention of this post, however, is to make contact with the models which we have implemented so far, we will dig a bit deeper and start directly with a model instead.

In the transformers library, pretrained models are usually downloaded from the hub and identified by name, which – by convention – is the name of the provider followed by a slash and the name of the model. Here is a short code snippet that you can execute in a notebook or in an interactive Python session which will download the weights for the 1.3 billion parameter version of the GPT-Neo model. GPT-Neo is a series of models developed and trained by EleutherAI and made available as open source, including the weights. 

import transformers
import torch
model_name="EleutherAI/gpt-neo-1.3B"
model = transformers.AutoModelForCausalLM.from_pretrained(model_name)
print(model)
print(isinstance(model, torch.nn.Module))

Executing this for the first time will trigger the download of the model to ~/.cache/huggingface/hub. The entire download is roughly 5 GB MB, so this might take a second. If you want to avoid the large download, you can also use the much smaller 125m version – just change the last part of the model name accordingly. From the output, we can see that this model is a torch.nn.Module, so we can use it as any other PyTorch model.

We can also see that the model actually consists of two components, namely an instance of the class GPTNeoModel defined here and a linear layer – the so-called head – that is sitting on top of the actual transformer and, as usual, transforms between the model inner dimension which is 2048 and the one-hot encoded vocabulary. This decomposition of the full model into a core model and a task-specific head is common to most Huggingface models, as it allows us to use the same set of weights for different tasks.

Even though the model does not use the transformer blocks that are part of PyTorch, it is a decoder-only transformer model as we would expect it – there are two learned embeddings for positions and words and 24 transformer blocks consisting of self-attention and linear layers. There is a minor difference, though – every second layer in the GPT-Neo model uses local self-attention, which basically means that to calculate the attention at a given position, only keys and values within a sliding window are used, not all keys and values in the context – see the comment here.

Apart from this, our model is very close to the models that we have implemented and trained previously. We know how to sample from such a model. But before we can do this, we need to turn our attention to the second part of a pipeline, namely the tokenizer.

Obviously, a pretrained transformer model will only produce reasonable results if we use the same vocabulary and the same tokenizer for inference that we have used for training. Therefore, the Huggingface hub contains a matching tokenizer for every pretrained model. This tokenizer can be downloaded and initialized similar to what we have done for the model.

tokenizer = transformers.AutoTokenizer.from_pretrained(model_name)

Our tokenizer will contain everything that we need to convert forth and back between text and sequences of token. Specifically, the main components of a tokenizer are as follows.

First, there is method encode which accepts a text and returns a sequence of token IDs, and a method decode which conversely translates a sequence of token IDs into a text.

To convert between the string representation of a token and the ID, there are the methods convert_ids_to_tokens and convert_tokens_to_ids. In addition, the tokenizer obviously contains a copy of the vocabulary and some special token like a token that marks the end of a sentence (EOS token), the beginning of a sentence (BOS token), unknow token and so forth – this should in general match the token defined in the model config model.config

In our case, the tokenizer is an instance of the GPT2 tokenizer which in turn is derived from the PretrainedTokenizer class.

Having a tokenizer at our disposal, we can now sample from the model in exactly the same way as from our own models. There are two little details that we need to keep in mind. First, in the Huggingface world, the batch dimension is the first dimension. Second, the forward method of our model returns a dictionary in which the logits are stored under a key with the same name. Also, the context size is part of the model config and called max_position_embeddings. Thus our sampling method looks as follows, assuming that we have a method do_p_sampling that draws from a distribution p. 

def predict(model, prompt, length, tokenizer, temperature = 0.7,  p_val = 0.95):
    model.eval()
    with torch.no_grad():
        sample = []
        device = next(model.parameters()).device
        #
        # Turn prompt into sequence of token IDs
        # 
        encoded_prompt  = tokenizer.encode(prompt)        
        encoded_sample = encoded_prompt
        encoded_prompt = torch.tensor(encoded_prompt, dtype = torch.long).unsqueeze(dim = 0)
        with torch.no_grad():
            out = model(encoded_prompt.to(device)).logits # shape B x L x V
            while (len(encoded_sample) < length):
                #
                # Sample next character from last output. Note that we need to remove the
                # batch dimension to obtain shape (L, V) and take the last element only
                #
                p = torch.nn.functional.softmax(out[0, -1, :] / temperature, dim = -1)
                #
                # Sample new index and append to encoded sample
                #
                encoded_sample.append(do_p_sampling(p, p_val))
                #
                # Feed new sequence
                #
                input = torch.tensor(encoded_sample[-model.config.max_position_embeddings:], dtype=torch.long)
                input = torch.unsqueeze(input, dim = 0)
                out = model(input.to(device)).logits
                print(tokenizer.decode(encoded_sample))

        return tokenizer.decode(encoded_sample)

This works, but it is awfully slow, even on a GPU. There is a reason for that, which is similar to what we have observed when sampling from an LSTM.

Suppose that our prompt has length L, and that we have already sampled the first token after the prompt, so that our full sample now has length L + 1. We now want to sample the next token. For that purpose, we only need the logits at position L + 1, so it might be tempting to feed only token L + 1 into our model. Let us quickly recall why this does not work.

To derive the output at position L + 1, each attention block will run the attention value at position L + 1 (which is a tensor of shape B x V) through the feed-forward network. If q denotes the query at position L + 1, this attention value is given by

\frac{1}{\sqrt{d}} \sum_{i=0}^{L} (q \cdot k_i) v_i

So we see that we need all keys and values to calculate the attention – which is not surprising, as this is the way how the model takes the context into account – but the query is only needed for position L + 1 (which is index 0, as we use zero-based indexing). Put differently, the only reason why we need to feed the previously generated token again and again into the model is that we need to key and value pairs from the past.

This hints at an opportunity to speed up inference – we could try to cache these values. To realize this, the Huggingface model returns the keys and values of all layers as an item past_key_values in the output and allows us to provide this as an additional argument to the next call. Thus instead of passing the full tensor of input IDs of length L + 1, we can as well pass only the last value, i.e. the ID of the currently last token, plus in addition the key value pairs from the previous call. Here is the updated sampling function.

def predict(model, prompt, length, tokenizer, temperature = 0.7,  p_val = 0.95):
    model.eval()
    with torch.no_grad():
        sample = []
        device = next(model.parameters()).device
        #
        # Turn prompt into sequence of token IDs
        # 
        encoded_prompt  = tokenizer.encode(prompt)        
        encoded_sample = encoded_prompt
        input_ids = torch.tensor(encoded_prompt, dtype = torch.long).unsqueeze(dim = 0)
        with torch.no_grad():
            #
            # First forward pass- use full prompt
            #
            out = model(input_ids = input_ids.to(device))
            logits = out.logits[:, -1, :] # shape B x V
            past_key_values = out.past_key_values
            while (len(encoded_sample) < length):
                #
                # Sample next character from last output
                #
                p = torch.nn.functional.softmax(logits[0, :] / temperature, dim = -1)
                #
                # Sample new index and append to encoded sample
                #
                idx = do_p_sampling(p, p_val)
                encoded_sample.append(idx)
                #
                # Feed new token and old keys and values
                #
                input_ids = torch.tensor(idx).unsqueeze(dim = 0)
                out = model(input_ids = input_ids.to(device), past_key_values = past_key_values)
                logits = out.logits
                past_key_values = out.past_key_values
                print(tokenizer.decode(encoded_sample))

        return tokenizer.decode(encoded_sample)

This should be significantly faster and provide a decent performance even on a CPU – when running this, you will also realize that the first pass that feeds the entire prompt takes some time, but all subsequent passes are much faster.

That closes our post for today. We have bridged the gap between the models that we have implemented and trained so far and the – much more advanced – models on the Huggingface hub and have convinced ourselves that even though these models are of course much larger and more powerful, their architecture is the same as for our models, and we can use them in the same way. I encourage you to play with a few other models which can be sampled from in exactly the same way, like the Pythia models from EleutherAI or the gpt2-medium and gpt2-large versions of the GPT model that can all be found on the Huggingface hub – you can use the code snippets from this post or my notebook as a starting point.

In the next post, we will use the popular Streamlit platform to implement a simple ChatBot backed by a Huggingface model.

Mastering large language models – Part XIII: putting it all together

Today, we will apply what we have learned in the previous posts on BPE, attention and transformers h- we will implement and train a simple decoder-only transformer model from scratch.

First, let us discuss our model. The overall structure of the model is in fact quite similar to the model we have used when training an LSTM on “War and Peace” – we will have an embedding layer turning words into vectors, the actual network and an output layer of the dimension of the vocabulary from which we will sample our next word. However, there are a few notable differences.

The most obvious and most important one is that we use a transformer instead of an LSTM. More specifically, we will use a decoder-only model, i.e. there is no input from an encoder. Instead, the model applies self-attention on the input in each layer. Recall that technically, the transformer blocks in this model will be instances of torch.nn.TransformerEncoderLayer even though we will use them as decoder building blocks. We will also have to use masking to avoid that our model can peek ahead in the self-attention layers.

The second difference is that instead of character-level encoding, we will apply a BPE tokenizer trained with a fixed number of merges. We will use sinusoidal positional embeddings as in the original transformer paper. With these modifications, our model looks as follows.

Using the sinusoidal embeddings discussed in one of our previous posts, we can now easily code our model in Python.

class Model(torch.nn.Module):
    
    def __init__(self, vocab_size, model_dim = MODEL_DIM, context_size = CONTEXT_SIZE, ff_dim = FF_DIM, heads = HEADS, layers = LAYERS, dropout = DROPOUT):
        super().__init__()
        self._word_embedding = torch.nn.Embedding(vocab_size, model_dim)
        self._pe_embedding = PosEmbeddingLayer(context_size, model_dim)
        layer = torch.nn.TransformerEncoderLayer(d_model = model_dim, nhead = heads, dim_feedforward = ff_dim, dropout = dropout)
        self._transformer = torch.nn.TransformerEncoder(layer, num_layers = layers)
        self._linear = torch.nn.Linear(in_features = model_dim, out_features = vocab_size)
        self._model_dim = model_dim
        self._context_size = context_size
        self._vocab_size = vocab_size
        cached_mask = torch.tril(torch.ones(context_size, context_size)*(-1)*float('inf'), diagonal = -1).t()
        self.register_buffer("_cached_mask", cached_mask)
    
    #
    # Create a causal self-attention mask
    #
    def get_self_attention_mask(self):
        return self._cached_mask
        
    #
    # Shape of input: (L, B)
    # 
    def forward(self, x):
        assert len(x.shape) == 2, "Expecting two-dimensional input"
        (L, B) = x.shape
        x = self._word_embedding(x) # shape (L, B, model_dim)
        x = self._pe_embedding(x) 
        #
        # Mask input. As we have registered this is a buffer, it
        # should already be on the same device as the model
        #
        mask = self.get_self_attention_mask()[:L, :L]
        x = self._transformer(x, mask = mask)
        return self._linear(x)

Note the causal self-attention mask that we use. In order to avoid having to recalculate this mask for every input, we create the mask once and add it as a buffer to the model, which will ensure that the mask will also be transferred if we move our model to the GPU.

We also follow the convention to use the second dimension as batch dimension. So our initial input will have shape (L, B), where each column of length L is a tensor whose elements are the indices of a token in the vocabulary, which we then pass through the embedding layers to obtain a tensor of shape (L, B, D). We then pass this through all transformer layers and finally through the output layer which will project this back into the vocabulary, i.e. we now have a tensor of shape (L, B, V). As usual, we do not include the final softmax, so that we have to apply the softmax before we sample.

Let us now discuss our dataset and the preprocessing. As for our word2vec example, we will use the WikiText dataset. This dataset comes in two flavors: WikiText2 with a bit more than 2 million token and WikiText103 with a bit more than 100 million token. During preprocessing, we need to pre-tokenize the dataset, build a BPE vocabulary and a rule set from it, encode the data and finally split it into a training dataset and a validation dataset. Training then proceeds as usual using teacher forcing. As in the GPT-3 paper, we use a cosine learning rate schedule to decrease the learning rate over time from its original value by 90%.

If you want to train the model from scratch but do not have access to a CUDA-enable machine, you can play with the notebook that I have created for this post on Google CoLab. For this notebook, I use the smaller WikiText2 dataset and train for only three epochs. The runtime does of course depend on the GPU (and the CPU) that Google will assign to your runtime. When I tried this, running the BPE merge and encoding the entire dataset took roughly 5 minutes in total, and the training took less than 30 minutes.

Here is a short sample created using the model trained on Google CoLab (which you can also find in the notebook itself).

Federer also received the first title of the Australian Open in the finals, including the Madonna Open, the Duke of Florence, and his first tournament. Federer won the final, losing to the finals, having scored a record nine times to five consecutive weeks before losing 19, in the Bir ‘Shoot , an injury

Of course this does not really make sense, but is still a bit impressive for less than 30 minutes of training. Most parts of this sentence are grammatically meaningful, and some snippets do even sound reasonable.

To get better results, we can try to train the model on a larger dataset, for instance the full WikiText103 data set instead of the small WikiText2 dataset. This goes beyond what we can reasonably do with a free GPU on Google CoLab. If, however, you have access to a decent GPU, you can do the training yourself. To create the training dataset, run the following commands (after activating a matching Python environment as described in the README)

#
# Clone repository if not yet done
#
git clone https://github.com/christianb93/MLLM
cd MLLM/wiki
#
# Remove existing data and run preprocessing
#
rm -f vocab.dat rules.data data.json
python3 preprocess.py

This takes a few minutes as we will have to build a BPE vocabulary and encode the entire dataset (do not trust the initial ETCs during encoding – as we implement a cache, the speed will go up with every word already decoded, and the entire process should take around 15 – 20 min, depending of course on your environment). The results of the preprocessing are five files – the vocabulary vocab.dat, the merge rules rules.dat, the fulll encoded dataset data.json as well as files train.json and val.json for training and validation (if the vocabulary, rules and data file exist, they will be reused, so make sure to remove existing copies if you do not want this).

Once the preprocessing is complete, we can start the training. I trained the model for two epochs on an A10 machine on Lambdalabs, using the command

python3 train.py --epochs=2 --compile --autocast

On this machine, one batch took 0.05 seconds, resulting in a runtime of 7.5 hours for two epochs. I have added the resulting model checkpoint model.pt to the repository (make sure to delete this file if you want to train from scratch, as otherwise training will restart from this file).

We can now sample from the model (either from the pretrained model or from a model from a custom training run) by simply running

python3 predict.py

By default, this will apply nucleus sampling with p=0.95 and a temperature of 0.7. Here is an output generated using the pretrained model that is part of the repository.

His wedding did not hear the explanation of the title, as his term ” Alan Keegan ” was in a press release. The first episode was broadcast on July 13, 2007. The episode was written by Matt Groening, and was written by Stella Packard. The episode was broadcast on BBC One in the United States on July 11, 2009, and was watched by 2. 93 million viewers, and it was watched by 7. 50 million viewers in the United States. It was the first time that the episode was viewed by 4. 21 million viewers and was viewed by 4. 3 million households. The episode received a 3. 1 rating / 9 share among viewers between the ages of 18 and 49. The episode was watched by approximately 7. 8 million viewers. It received generally positive reviews from television critics. It received generally positive reviews from television critics, according to Nielsen Media Research…

The first sentence does not make too much sense, but the second and the next few sentences do at least make partial sense. We also see, however, that the model tends to repeat itself, which is probably due to the comparatively low temperature. Here is another sample generated with temperature 0.9.

The series was a single nine – part series against Ivor on its official website. Two seasons earlier, the original series was released on May 2, 2014, was released as a partnership with Clifton Notes in the United States. These were a number of reprint edition hardcover footage. Many reviews were positive and negative and positive. Loves made Yerne the first film in the series by Dirty, featuring Beyoncé ‘s voice acting. The lead character Ron Fisk of Hope called the film ” a rogue look inside “. Lyrically, the crew got off in a course at the end of the scene. Sacred Kimball, who played by the actors of the film, left England at the end of the episode, was shot in a short story of a movie about that film. The film was influenced by David Duchovny

Clearly, this is still not GPT – on the other hand, our model is tiny (it has only roughly 5 million parameters, compared to the 175 billion parameters used for GPT-3) and so is our data (a bit more than 100 million token, whereas GPT-3 was trained on more than 300 billion token). Theoretically, we could now proceed to train larger models on more data, but the cost associated with the required infrastructure will soon become prohibitive.

Fortunately, a few models and weights are available to the public. Probably the easiest way to download and run these models is the Huggingface Transformers library. In our next post, we will start to work with this library to download popular models like GPT-2 and play with them.

Mastering large language models – Part XII: byte-pair encoding

On our way to actually coding and training a transformer-based model, there is one last challenge that we have to master – encoding our input by splitting it in a meaningful way into subwords. Today, we will learn how to do this using an algorithm known as byte-pair encoding (BPE).

Let us first quickly recall what the problem is that subword encoding tries to solve. To a large extent, the recent success of large language models is due to the tremendous amount of data used to train them. GPT-3, for instance, has been trained on roughly 500 mio tokens (which, as we will see soon, are not exactly words) [3]. But even much smaller datasets tend to contain a large number of unique words. The WikiText103 dataset [4] for instance contains a bit more than 100 mio. words, which represent a vocabulary of 267.735 unique words. With standard word-level encoding, this would become a dimension in the input and output layers of our neural network. It is not hard to imagine that with 500 mio. token as input, this number would even be much larger and we clearly have a problem.

The traditional way to control the growth of the vocabulary is to introduce a minimum frequency. In other words, we could only include token in the vocabulary that occur more than a given number of times – the minimum frequency – in the training data and tune this number to realize a cap on the vocabulary size. This, however, has the disadvantage that during training and later inference, we will face unknown words. Of course we can reserve a special token for these unknown words, but still a translator would have to know how to handle them.

Character-level encoding solves the problem of unknown words, but introduces a new problem – the model first has to learn words before it can start to learn relations between words. In addition, if our model is capable of learning relations within a certain range L, it does of course make a difference whether the unit in which we measure this range is a character or a word.

This is the point where subword tokenization comes into play. Here, the general idea is to build up a vocabulary that consists of subword units, not full words – but also more than just individual characters. Of course, to make this efficient, we want to include those subwords in our vocabulary that occur often, and we want to include all individual characters. If we need to encode a word that consists of known subwords, we can use those, and in the worst case, we can still go down to the character level during encoding so that we will not face unknown words.

Byte-pair encoding that has first been applied to machine learning in [1] is one way to do this. Here, we build our vocabulary in two phases. In the first phase, we go through our corpus and include all characters that we find in our vocabulary. We then encode our data using this preliminary vocabulary.

In the second phase, we iterate through a process known as merge. During each merge, we go through our data and identify the pair of token in the vocabulary that occurs most frequently. We then include a new token in our vocabulary that is simply the concatenation of these two existing token and update our existing encoding. Thus every merge adds one more token to the vocabulary. We continue this process until the vocabulary has reached the desired size.

Note that in a real implementation, the process of counting token pairs to determine their frequency is usually done in two steps. First, we count how often an individual word occurs in the text and save this for later reference. Next, given a pair of token, we go through all words that contain this pair and then add up the frequencies of these words to determine the frequency of the token pair.

Let us look at an example to see how this works in practice. Suppose that the text we want to encode is

low, lower, newest, widest

In the first phase, we would build an initial vocabulary that consists of all characters that occur in this text. However, we want to make sure that we respect word boundaries, so we need to be able to distinguish between characters that appear within a word and those that appear at the end of the word. We do this by adding a special token </w> to a token that is located at the end of a word. In our case, this applies for instance to the character w that therefore gives rise to two entries in our vocabulary – w and w</w>. With this modification, our initial vocabulary is

'o', 'r</w>', 's', 'w</w>', 'n', 'i', 'e', 'l', 'd', 'w', 't</w>'

We now go through all possible combinations of two token and see how often the appear in the text. Here is what we would find in our example.

Token pairFrequency
l + o2
o + w</w>1
o + w1
w + e2
e + r</w>1
n + e1
e + w1
e + s2
s + t</w>2
w + i1
i + d1
d + e1

We now pick the pair of token (usually called a byte-pair, even though this is strictly speaking of course not correct when we use Unicode points) that occurs most frequently. In our case, several byte pairs occur twice, and we pick one of them, say w and e. We now add an additional token “we” to our vocabulary and re-encode our text. With this vocabulary, our text which previously was represented by the sequence of token

l, o, w</w>, l, o, w, e, r</w>, n, e, w, e, s, t</w>, w, i, d, e, s, t</w>

would now be encoded as

l, o, w</w>, l, o, we, r</w>, n, e, we, s, t</w>, w, i, d, e, s, t</w>

Note the new token, marked with bold face, that appears at the two positions where we previously had the combination of the token w and e. This concludes our first merge.

We can now continue and conduct the next merge. Each merge will add one token to our vocabulary, so that controlling the number of merges allows us to create a vocabulary of the desired size. Note that each merge results in two outputs – an updated vocabulary and a rule. In our case, the first merge resulted in the rule w, e ==> we.

To encode a piece of text that was not part of our training data when running the merges, we now simply replay these rules, i.e. we start with our text, break it down into characters, corresponding to the token in the initial vocabulary, and apply the rules that we have derived during the merges in the order in which the merges took place. Thus to encode text, we need access to the vocabulary and to the rules.

Let us now turn to implementing this in Python. The original paper [1] does already contain a few code snippets that make an implementation based on them rather easy. As usual, this blog post comes with a notebook that, essentially based on the code in [1], guides you through a simple implementation using the example discussed above. Here are a few code snippets to illustrate the process.

The first step is to build a dictionary that contains the frequencies of individual words, which we will later use to easily calculate the frequency of a byte pair. Note that the keys in this dictionary are the words in the input text, but already broken down into a sequence of token, separated by spaces, so that we need to update them as we merge and add new token.

def get_word_frequencies(pre_tokenized_text):
    counter = collections.Counter(pre_tokenized_text)
    word_frequencies = {" ".join(word) + "</w>" : frequency for word, frequency in counter.items() if len(word) > 0}
    return word_frequencies

As the keys in the dictionary are already pretokenized, we can now build our initial vocabulary based on these keys. 

def build_vocabulary(word_frequencies):
    vocab = set()
    for word in word_frequencies.keys():
        for c in word.split():
            vocab.add(c)
    return vocab

Next, we need to be able to identify the pair of bytes that occurs most frequently. Again, Python collections can be utilized to do this – we simply go through all words, split them into symbols, iterate through all pairs and increase the count for this pair that we store in a dictionary.

def get_stats(word_frequencies):
  pairs = collections.defaultdict(int)
  for word, freq in word_frequencies.items():
    symbols = word.split()
    for i in range(len(symbols)-1):
      pairs[symbols[i],symbols[i+1]] += freq
  return pairs

Finally, we need a function that executes an actual merge. During each merge, we use regular expressions (more on the exact expression that we use here can be found in my notebook) to replace each occurence of the pair by the new token. 

def do_merge(best_pair, word_frequencies, vocab):
    new_frequencies = dict()
    new_token = "".join(best_pair)
    pattern = r"(?<!\S)" + re.escape(" ".join(best_pair)) + r"(?!\S)"
    vocab.add(new_token)
    for word, freq in word_frequencies.items():
        new_word = re.sub(pattern, new_token, word)
        new_frequencies[new_word] = word_frequencies[word]
    return new_frequencies, vocab

We can now combine the functions above to run a merge. Essentially, during a merge, we need to collect the statistics to identify the most frequent pair, call our merge function to update the dictionary containing the word frequencies and append the rule that we have found to a list of rules that we will save later.

stats = get_stats(word_frequencies)
best_pair = max(stats, key=lambda x: (stats[x], x)) 
print(f"Best pair: {best_pair}")
word_frequencies, vocab = do_merge(best_pair, word_frequencies, vocab)
rules.append(best_pair)

This code, howevers, is awfully slow, as it basically repeats the process of counting once with every merge. The authors of the original paper also provide a reference implementation [2] that applies some tricks like caching and the use of indices to speed up the process significantly. In my repository for this series, I have assembled an implementation that follows this reference implementation to a large extent, but simplifies a few steps (in particular the incremental updates of the frequency counts) and is therefore hopefully a bit easier to read. The code consists of the main file BPE.py and a test script test bpe.py.

The test script can also be used to compare the output of our implementation with the reference implementation [3]. Let us quickly do this using a short snippet from “War and peace” that I have added to my repository.

#
# Clone the reference implementation
#
git clone https://github.com/rsennrich/subword-nmt.git
cd subword-nmt
#
# Get files from my repository
#
wget https://raw.githubusercontent.com/christianb93/MLLM/main/bpe/BPE.py
wget https://raw.githubusercontent.com/christianb93/MLLM/main/bpe/test_bpe.py
wget https://raw.githubusercontent.com/christianb93/MLLM/main/bpe/test.in
wget https://raw.githubusercontent.com/christianb93/MLLM/main/bpe/test.rules
#
# Run unit tests
# 
python3 test_bpe.py
#
# Run reference implementation
#
cat test.in | python3 subword_nmt/learn_bpe.py -s=50 > rules.ref
#
# Run our implementation
#
python3 test_bpe.py --infile=test.in --outfile=rules.dat
#
# Diff outputs
#
diff rules.dat rules.ref
diff rules.ref test.rules

The only difference that the diff should show you is a header line (containing the version number) that the reference implementation adds which we do not include in our output, all the remaining parts of the output files which contain the actual rules should be identical. The second diff verifies the reference file that is part of the repository and is used for the unit tests.

Over time, several other subword tokenization methods have been developed. Two popular methods are Googles wordpiece model ([6], [7]) and the unigram tokenizer [8]. While wordpiece is very similar to BPE and mainly differs in the way how the next byte pair for merging is selected, the unigram tokenizer starts with a very large vocabulary, containing all characters and the most commonly found substrings, and then iteratively removes items from the vocabulary based on a statistic model.

With BPE, we now have a tokenization method at our disposal which will allow us to decouple vocabulary size from the size of the training data, so that we can train a model even on large datasets without having to increase the model size. In the next post, we will put everything together and train a transformer-based model on the WikiText dataset.

References:

[1] R. Sennrich et al., Neural Machine Translation of Rare Words with Subword Units
[2] https://github.com/rsennrich/subword-nmt
[3] T. Brown et al., Language Models are Few-Shot Learners
[4] https://blog.salesforceairesearch.com/the-wikitext-long-term-dependency-language-modeling-dataset/
[5] K. Bostrom, G. Durrett, Byte Pair Encoding is Suboptimal for Language Model Pretraining
[6] Y. Wu et al., Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation
[7] M. Schuster, K. Nakajima, Japanese and Korean voice search
[8] T. Kudo, Subword Regularization: Improving Neural Network Translation Models with Multiple Subword Candidates

Mastering large language models – Part XI: encoding positions

In our last post, we have seen that the attention mechanism is invariant to position, i.e. that reordering of the words in a sentence yields the same output, which implies that position information is lost. Clearly position information does matter in NLP, and therefore transformer based models apply positional embeddings in addition to the pure word embeddings.

Before explaining positional embeddings, let us first recall word embeddings in general. Suppose we are working with sentences consisting of L token taken out of a fixed vocabular. Then creating vectors out of these token amounts to map each token

token_1, token_2, token_3, \dots, token_L

to a vector vi. This encoding, however, is usually position independent, meaning that if the same token appears at two different positions in the sentence, the resulting vector will be the same for both instances of the token. Technically, the embedding can be described by a matrix of dimension (D, V), where D is the model dimension and V is the size of the vocabulary, and each column in this matrix represents the embedding for one token.

In the original transformer paper [1], these word embeddings are augmented by an additional positional embedding. Similar to word embeddings, this again attaches a vector of dimension D to every token in the input. However, this embedding now solely depends on the position of the token, and not on the actual token itself, so that different token at the same position yield the same embedding. This additional embedding is then added to the word embedding to obtain one vector per token which is then fed into the actual model.

But what is the vector that we want to add to the word embedding at position i? Obviously, there are many choices (reference [3] is a good survey of existing approaches). The approach taken in the original transformer is to use fixed values which are not learned and not modified during training and are given by the equations

\textrm{PE}(p, i) = \begin{cases} \sin(C^{i / D} p) & i \, \textrm{even} \\ \cos(C^{(i-1) / D} p) & i \, \textrm{odd} \end{cases}

where C is a fixed constant (actually 1 / 10000), p is the position of the token in the sentence and i is the vector index, so that PEp or PE(p, : ) in Python notation is the vector added to the word embedding of a token at position p. Here we assume that the model dimension D is an even number.

The motivation provided for this specific choice in [1] is that for a fixed offset k, the positional encoding vectors PEp+k and PEp are related by a linear transformation, so that, as the authors phrase it in section 3.5 of [1], “it would allow the model to easily learn to attend by
relative positions“. Let us quickly verify this. For any i, component 2i of the vector PEp+k is given by

\begin{aligned}PE_{p+k, 2i} &= \sin(C^{2i / D} (p+k)) \\ &= \sin(C^{2i/D}p) \cos(C^{2i/D}k) + \cos(C^{2i/D}p) \sin(C^{2i/D}k) \\ &= \cos(C^{2i/D}k) PE_{p,2i} + \sin(C^{2i/D}k) PE_{p,2i+1} \end{aligned}

and similarly, the component 2i+1 is given by

\begin{aligned} PE_{p+k,2i+1} &= \cos(C^{2i / D} (p+k)) \\ &= \cos(C^{2i / D}p)\cos(C^{2i / D}k) - \sin(C^{2i / D}p)\sin(C^{2i / D}k) \\ &= \cos(C^{2i / D}k)PE_{p,2i+1} - \sin(C^{2i / D}k)PE_{p,2i} \end{aligned}

proving our claim. Note that these two relations can nicely be organized into one equation as

\begin{pmatrix} PE_{p+k, 2i} \\ PE_{p+k, 2i+1} \end{pmatrix} = \begin{pmatrix} \cos(C^{2i / D}k) & \sin(C^{2i / D}k) \\ - \sin(C^{2i / D}k) & \cos(C^{2i / D}k) \end{pmatrix} \begin{pmatrix} PE_{p, 2i} \\ PE_{p, 2i+1} \end{pmatrix}

showing that the two vectors are related by a rotation (we will get back to this point later when we talk about relative embeddings).

Let us quickly see how we could code this in Python. As we need one embedding vector of dimension D for each position, the embeddings form a matrix of shape (L, D), where each row represents one position. After applying the word embeddings to an input sequence of length L, this will as well result in a matrix of shape (L, D), and we can simply add these two matrices together. Of course, we would not calculate the sine and cosine values above again for every input, but store them in a global variable, an attribute or (better) in a PyTorch buffer. Here is a piece of code to calculate the embeddings, taken from the corresponding section in d2l.ai (note that this only works if D is even, which, however, is usually the case – in fact, dimensions are often multiples of 8, 16 or 32 to better support the inner workings of modern GPUs).

#
# Values for p and 2*i / D
#
_p = torch.arange(L , dtype=torch.float32).unsqueeze(dim = 1)
_i = torch.arange(0, D , step = 2) / D
#
# x = C**(2i/D)*p
#
x = torch.pow(C, _i) * _p
#
# Apply sine and cosine and organize into a matrix pe
#
pe = torch.zeros(L, D)
pe[:, 0::2] = torch.sin(x)
pe[:, 1::2] = torch.cos(x)

For more on this and a few visualisations, you might want to take a look at the notebook for this post.

Note that at this point, we need to make an assumption on the maximum length of the input sequence that we will be using, called the context size. The context size is also an important parameter for training and inference, as the attention matrices have shape (L, L), so that a large context size increases memory usage and computational complexity.

As already mentioned, this way to construct embeddings is not the only one. A second method that has gained some popularity and is for instance applied in GPT-models ([4]) is to use learned embeddings. With this approach, the positional embeddings are treated similarly to the word embeddings, i.e. they are simply parameters that are initialized with some random values and then updated during backward passes as any other parameter of the network.

Both the sinusoidal embeddings used in the original transformer paper as well as the learned embeddings used by GPT are absolute embeddings, i.e. the value of an embedding depends on the absolute position of a token in a sentence. In [2], a different approach is taken which is known as relative embeddings and relies on a modification of the self-attention mechanism to incorporate positional information rather than on absolute positional embeddings added to the word embeddings before processing them in the attention layer.

More specifically, when calculating attention scores and before applying the softmax, the usual dot product between query at position i and key at position j is modified by adding a bias vector w to the key that depends on the relative position, i.e. the difference j – i.

q \left( \cdot k^t + w_{j-i}\right)

These bias vectors are then learned, similar to the word embeddings. This modification is applied not only in the first layer, but in all layers. In addition, to avoid having to learn 2*L embeddings for each layer and each attention head, the authors clip the relativ position, i.e. instead of using the index j – i which can range from -L to L, the use the modified index

\max(-k, \min(k, j-i))

so that the relative position is clipped to values between -k and k, where k is a hyperparameter. For an efficient implementation, see [5].

Many variations of this approach are possible. An interesting example is the T5 model described in [6] which we will look at in more detail in a later post. In this model, the position dependent vector added to the key before taking the dot product with the query is replaced by a scalar added after taking the dot product, so that the dot product is replaced by

q \cdot k^t + a_{j-i}

where aj-i is now a scalar. These scalars are again learned parameters, shared between different layers but unique for each head. Instead of a clipping, buckets are formed, each corresponding to a range of different values of j – i. so that the number of parameters that need to be learned is simply the number of buckets times the number of heads. It is instructive to take a look at the T5 implementation of the Huggingface Transformer library to see how this works in practice – the notebook for this post contains a simplified and commented version of this code.

Before moving on, let us quickly discuss another type of relative positional embeddings known as rotary embeddings, originally proposed in [7]. In contrast to the approaches that we have seen so far, this method does not modify the self-attention score by adding a vector or scalar, but by rotating queries and keys before forming the dot product. Specifically, the authors consider a set of orthogonal matrices

R_{\Theta, i}

depending on a fixed parameter Θ and the position i and replace the usual attention dot product between query and key by

q_i R_{\Theta, i} (k_j R_{\Theta, j})^t = q_i R_{\Theta, i} R_{\Theta, j}^t k_j^t

At the first glance, this does not seem to be a relative embedding, as it seems to depend on both positions – the position i of the query and the position j of the key. However, the authors choose a set of matrices that mathematically speaking form something resembling a one-parameter subgroup, i.e. having the property that

R_{\Theta, i} R_{\Theta, j}^t = R_{\Theta, i - j}

so that the attention score is actually

q_i R_{\Theta, i - j} k_j^t

which does in fact only depend on the difference i – j, i.e. on the relative position of query and key. Rotary embeddings have also been applied in the GPT-NeoX model by EleutherAI.

We now have a broad selection of different embedding methods to our disposal and could go ahead and apply them to train a transformer-based decoder-only model. However, there is still some challenge that we have not touched upon – the word encodings. So far, our word encodings were straightforward – we did either chose to turn each individual character into a token or used word-based encodings where our vocabulary consists of all words found in the training data. Unfortunately, both approaches have certain drawbacks. Character-based encodings imply that the model also has to learn how to assemble words from characters and makes learning long-range relations more difficult. Word-based encodings suffer from the problem that the number of unique words in the training data can become huge, which will blow up our model size.

For that reason, many models use a third approach known as subword tokenization, where token are built from parts of words instead of individual characters or entire words. In the next post, we will therefore study the tokenization mechanism used by the original transformer – byte-pair encoding (BPE).

References:

[1] A. Vaswani et al., Attention is all you need
[2] P. Shaw et al., Self-Attention with Relative Position Representations
[3] P. Dufter, M. Schmitt, H. Schütze; Position Information in Transformers: An Overview. Computational Linguistics 2022; 48 (3): 733–763
[4] A. Radford et al., Improving Language Understanding by Generative Pre-Training
[5] C. Huang et al, Music Transformer: generating music with long-term structure
[6] C. Raffel et al., Exploring the Limits of Transfer Learning with a Unified
Text-to-Text Transformer
[7] J. Su et al., RoFormer: Enhanced Transformer with Rotary Position Embedding

Mastering large language models – Part X: Transformer blocks

Today, we will start to look in greater detail at the transformer architecture. At the end of the day, a transformer is built out of individual layers, the so-called transformer blocks, stacked on top of each other, and our objective for today is to understand how these blocks are implemented.

Learning about transformer architectures can be confusing. If you read the original paper Attention is all you need by Vaswani et al. (and I highly recommend to actually take a look at the paper), you will, already on page 3, stumble upon a rather complicated diagram which is actually a bit intimidating if all of this is new to you. This paper talks about encoders and decoders, which is a language that we understand thanks to a previous post. On the other hand, you will hear statement that popular models like GPT-2 are in fact decoder-only models, without having a clear definition at hand what this actually means. To make things worse, decoder-only models are built out of PyTorch modules which, confusingly enough, are called torch.nn.TransformerEncoder. So before getting into too many details, let us first try to clean up that mess a bit.

The most general transformer models like the one described in the original paper or popular models like T5 are in fact encoder-decoder models. The general architecture is not so much different from the encoder-decoder models that we have already seen in the context of RNNs. There is a first network, the encoder, which translates a source sentence into a sequence of embeddings. Then, there is a second network that uses the output of the encoder as a context – typically called the memory in transformer-based architectures – to generate the source sequence. A crucial difference, though, is that the decoder reads the input of the encoder via an attention layer which gives the decoder network access to all time steps of the encoder at the same time. So very high-level, the picture is as follows.

Let us now dig a bit deeper. In fact, both, the encoder and the decoder, are built out of layers called transformer blocks. For the encoder, every transformer block has one input and one output. For the decoder, every transformer block has two inputs and one output. One input reads, via an attention mechanism, data from the encoder (more precisely, keys and values are taken from the encoder, while queries are taken from the decoder). The second input is taken from the previous transformer block of the encoder. So on the next level of detail, the diagram looks like this.

This explain the first (and most important) architectural difference between an encoder transformer block (torch.nn.TransformerEncoderLayer in PyTorch) and a decoder transformer block (torch.nn.TransformerDecoderLayer) – a decoder block has two inputs, an encoder block only one.

The second difference is the attention mask. Attention is actually applied at all inputs of a transformer block. For an encoder, masking is typically not done, so that the encoder can look at all token in the input. For the decoder, masking is also usually not done for the attention layer connecting the encoder and the decoder, so that the decoder has access to all time steps of the encoder output. For the second attention layer of a decoder, however, connected to the decoder input or the input of the previous layer, a causal self-attention mask is usually applied, i.e. the decoder is not allowed to peak ahead, as discussed in the last post. This difference, however, is not hardcoded into the PyTorch classes, as the attention mask in PyTorch is a parameter.

Finally, there are decoder-only transformers, and this is the class of transformer on which we will focus in the next few posts. These are transformers that are built from encoder blocks, each of which receives only one input, so there is no encoder. However, the attention mask used for the input is the one used for the decoder, so that we can apply teacher forcing to train such a model. Thus a decoder-only transformer receives a sequence of length L as input, encoded as a matrix of shape (L, D) where D is the embedding dimension, and produces an output of the same shape. If we add an embedding layer and an output layer, we can apply such a model for language generation very much in the same manner as an RNN, and this is the use case we will study first.

So let us talk about transformer blocks (more specifically, transformer blocks with only one input, i.e. encoder blocks in the PyTorch terminology) in more detail. Instead of jumping directly to the paper, let us take a different approach and look at the source code of the corresponding PyTorch module. The key lines in the forward method are

 x = self.norm1(x + self._sa_block(x, src_mask, src_key_padding_mask))
 x = self.norm2(x + self._ff_block(x))

Let us see what this does. First, we feed the input through a self-attention block. Note, however, that it is on us to specify a causal attention mask, as the model will not do this automatically.

Next, we apply a residual connection, i.e. we take the output of the self attention and add the original input to it. This helps to avoid vanishing gradients, as it allows a part of the gradient during backpropagation to flow directly back to the previous layer. Finally, we apply a layer normalization to the output, i.e. to the sum.

We then repeat the same pattern. This time, however, we run the result of the previous step through a feed-forward network before we again add the input to establish a residual connection and finally apply a normalization. Thus our full flow looks as follows.

So we repeat the pattern

\textrm{LayerNorm}(x + \textrm{Sublayer}(x))

twice, where first the sublayer is a self-attention layer and then the sublayer is a feed-forward network. This is, in fact, exactly the expression that we find in section 3.1 of the original paper.

Before we proceed, let us talk about dimensions. When working with transformers, it is common to present the input in the format (L, B, D), where L is the sequence length, B is the batch size and D is the dimension of the model. Each sublayer produces an output of the same shape, and so does the layer norm, so that the entire transformer block again produces an output of that shape.

In addition, a more careful look a the code shows that at the output of each sublayer, there is a dropout layer to avoid overfitting. As usual, the dropout is deactivated during inference and evaluation, but active during training.

So far, so good, but we are still missing an important point in our overall approach. To spot this, let us go ahead and quickly try out a transformer block in PyTorch, then permute the token in the input, i.e. change the orders of the input vectors, and run the new input through the transformer block again. Here is a short piece of code doing this (you can also have a look at the notebook that I prepared for this post.

# Model dimension
D = 8
# Length of encoder input
L = 4
#
# Create random input
#
X = torch.randn(L, D)
#
# and feed through an encoder block
#
block = torch.nn.TransformerEncoderLayer(d_model = D, nhead = 4)
block.eval()
Y = block(X).detach()
#
# Now permute the input, recompute
#
Xp = X.flip(dims = [0]).detach()
Yp = block(Xp).detach()
#
# Verify that Yp is simply the permutation of Y
#
print(f"{torch.allclose(Yp, Y.flip(dims = [0]))}")

We find that permuting the input to a transformer simply results in the same permutation applied to the output. This is not surprising after a closer look at the formula for the attention, but is not really matching our intuition of a good encoding of a sentence. After all, the two sentences

The dog chases the cat

and

The cat chases the dog

are permutations of each other, but have completely different meanings, so that from a good encoding, we would expect more than just a permutation as well. The problem becomes even more apparent if we now simulate the first step of processing that encoder output in a decoder, i.e. passing it through the attention layer connecting encoder and decoder. Recall that this attention layer uses keys and values from the encoder output, but the queries from the decoder input. Let us simulate this.

# length of target sequence, i.e. decoder input
T = 3 
queries = torch.randn(T, D)
attn = torch.nn.MultiheadAttention(embed_dim = D, num_heads = 4)
#
# Put into eval mode to avoid dropout
#
attn.eval()
#
# Values and keys are both the encoder output
#
out = attn(queries, Y, Y)[0].detach()
outp = attn(queries, Yp, Yp)[0].detach()
#
# Compare
#
print(f"{torch.allclose(out, outp)}")

This is even worse – the output is exactly the same, even after permuting the encoder input. That means that a transformer trying to translate the two sentences above would most likely produce the same target sentence, which we can also verify directly by using PyTorchs transformer module instead of its individual building blocks.

transformer = torch.nn.Transformer(d_model = D, nhead = 1)
transformer.eval()
tgt = torch.randn(T, D)
src = torch.randn(L, D)
src_permuted = src.flip(dims = [0])
out = transformer(src, tgt)
_out = transformer(src_permuted, tgt)
print(out)
print(_out)
print(f"{torch.allclose(out, _out)}")

So transformer models as discussed so far are not sensitive to the order of words in the input. To use them for NLP tasks, we therefore need an additional trick – positional embeddings – which we will discuss in the next post.

Mastering large language models – Part IX: self-attention with PyTorch

In the previous post, we have discussed how attention can be applied to avoid bottlenecks in encoder-decoder architectures. In transformer-based models, attention appears in different flavours, the most important being what is called self-attention – the topic of todays post. Code included.

Before getting into coding, let us first describe the attention mechanism presented in the previous blog in a bit more general setting and, along the way, introduce some terminology. Suppose that a neural network has access to a set of vectors vi that we call the values. The network is aiming to process the information contained in the vi in a certain context and, for that purpose, needs to condense the information specific to that context into a single vector. Suppose further that each vector vi is associated with a vector ki called the key, that somehow captures which information the vector vi contains. Finally assume that we are able to form a query vector q that specificies what information the network needs. The attention mechanism will then assemble a linear combination

\textrm{attn}(q, \{k_i\}, \{v_i\}) = \sum_i \alpha(q, k_i) v_i

called the attention vector.

To make this more tangible, let us look at an example. Suppose an encoder processes a sequence of words, represented by vectors xi. While encoding a part of the sentence, i.e. a specific vector, the network might want to pull in some data from other parts of the sentence. Here, the query would be the currently processed word, while keys and values would come from other parts of the same sentence. As keys, queries and values all come from the same sequence, this form of attention is called self-attention. Suppose, for example, that we are looking at the sentence (once again taken from “War and peace”)

The prince answered nothing, but she looked at him significantly, awaiting a reply

When the model is encoding this sentence, it might help to pull in the representation of the word “prince” when encoding “him”, as here, “him” refers to “the prince”. So while processing the token for “him”, the network might put together an attention vector focusing mostly on the token for “him” itself, but also on the token for “prince”.

In this example, we would compute keys and values from the input sequence, and the query would be computed from the word we are currently encoding, i.e. “him”. A weight is then calculated for each combination of key and query, and these weights are used to form the attention vector, as indicated in the diagram above (we will see in a minute how exactly this works).

Of course, this only helps if the weights that we use in that linear combination are somehow helping the network to focus on those values that are most relevant for the given key. At the same time, we want the weights to be non-negative and to sum up to one (see this paper for a more in-depth discussion of these properties of the attention weights which are a bit less obvious). The usual approach to realize this is to first define a scoring function

\textrm{score}(q, k_i)

and then obtain the attention weights as a softmax function applied to these scores, i.e. as

\alpha(q, k_i) = \frac{\exp(\textrm{score}(q, k_i))}{\sum_j \exp(\textrm{score}(q, k_j))}

For the scoring function itself, there are several options (see Effective Approaches to Attention-based Neural Machine Translation by Luong et al. for a comparison of some of them). Transformers typically use a form of attention called scaled dot product attention in which the scores are computed as

\textrm{score}(q, k) = \frac{q k^t}{\sqrt{d}}

i.e. as the dot product of query and key divided by the square root of the dimension d of the space in which queries and keys live.

We have not yet explained how keys, values and queries are actually assembled. To do this and to get ready to show some code, let us again focus on self attention, i.e. queries, keys and values all come from the same sequence of vectors xi which, for simplicity, we combine into a single matrix X with shape (L, D), where L is the length of the input and D is the dimensionality of the model. Now the queries, keys and values are simply derived from the input X by applying a linear transformation, i.e. by a matrix multiplication, using a learnable set of matrices weights WQ (for the queries), WV (for the values) and WK (for the keys).

Q = X W^Q
K = X W^K
V = X W^V

Note that the individual value, key and query vectors are now the rows of the matrices V, K and Q. We can therefore conveniently calculate all the scaled dot products in one step by simply doing the matrix multiplication

\frac{Q \cdot K^T}{\sqrt{d}}

This gives us a matrix of dimensions (L, L) containing the scores. To calculate the attention vectors, we now still have to apply the softmax to this and multiply by the matrix V. So our final formula for the attention vectors (again obtained as rows of a matrix of shape (L, D)) is

\textrm{attn}(Q, K, V) = \textrm{softmax}\left( \frac{Q \cdot K^T}{\sqrt{d}} \right) \cdot V

In PyTorch, this is actually rather easy to implement. Here is a piece of code that initializes weight matrices for keys, values and queries randomly and defines a forward function for a self-attention layer.

    
wq = torch.nn.Parameter(torch.randn(D, D))
wk = torch.nn.Parameter(torch.randn(D, D))
wv = torch.nn.Parameter(torch.randn(D, D))
    
#
# Receive input of shape L x D
#
def forward(X):
    Q = torch.matmul(X, wq)
    K = torch.matmul(X, wk)
    V = torch.matmul(X, wv)
    out = torch.matmul(Q, K.t()) / math.sqrt(float(D))
    out = torch.softmax(out, dim = 1)
    out = torch.matmul(out, V)
    return out

However, this is not yet quite the form of attention that is typically used in transformers – there is still a bit more to it. In fact, what we have seen so far is what is usually called an attention head – a single combination of keys, values and queries used to produce an attention vector. In real-world transformers, one typically uses several attention heads to allow the model to look for different patterns in the input. Going back to our example, there could be one attention head that learns how to model relations between a pronoun and the noun to which it refers. Other heads might focus on different syntactic or semantic aspects, like linking a verb to an object or a subject, or an adjective to the noun described by it. Let us now look at this multi-head attention.

The calculation of a multihead attention vector proceeds in three steps. First, we go through each of the heads which each has its own set of weight matrices (WQi, WKi, WVi) as before, and apply the ordinary attention mechanism that we have just seen to obtain a vector headi as attention vector for this head. Note that the dimension of this vector is typically not the model dimension D, but a head dimension dhead, so that the weight matrices now have shape (D, dhead). It is common, though not absolutely necessary, to choose the head dimension as the model dimension divided by the number of heads.

Next, we concatenate the output vectors of each head to form a vector of dimension nheads * dhead, where nheads is of course the number of heads. Finally, we now apply a linear transformation to this vector to obtain a vector of dimension D.

Here is a piece of Python code that implements multi-head attention as a PyTorch module. Note that here, we actually allow for two different head dimensions – the dimension of the value vector and the dimension of the key and query vectors.

class MultiHeadSelfAttention(torch.nn.Module):
    
    def __init__(self, D, kdim = None, vdim = None, heads = 1):
        super().__init__()
        self._D = D
        self._heads = heads
        self._kdim = kdim if kdim is not None else D // heads
        self._vdim = vdim if vdim is not None else D // heads
        for h in range(self._heads):
            wq_name = f"_wq_h{h}"
            wk_name = f"_wk_h{h}"
            wv_name = f"_wv_h{h}"
            wq = torch.randn(self._D, self._kdim)
            wk = torch.randn(self._D, self._kdim)
            wv = torch.randn(self._D, self._vdim)
            setattr(self, wq_name, torch.nn.Parameter(wq))
            setattr(self, wk_name, torch.nn.Parameter(wk))
            setattr(self, wv_name, torch.nn.Parameter(wv))
        wo = torch.randn(self._heads*self._vdim, self._D)
        self._wo = torch.nn.Parameter(wo)
        
    def forward(self, X):
        for h in range(self._heads):
            wq_name = f"_wq_h{h}"
            wk_name = f"_wk_h{h}"
            wv_name = f"_wv_h{h}"
            Q = X@getattr(self, wq_name)
            K = X@getattr(self, wk_name)
            V = X@getattr(self, wv_name)
            head = Q@K.t() / math.sqrt(float(self._kdim))
            head = torch.softmax(head, dim = -1)
            head = head@V
            if 0 == h:
                out = head
            else:
                out = torch.cat([out, head], dim = 1)
        return out@self._wo

We will see in a minute that this implementation works, but the actual implementation in PyTorch is a bit different. To see why, let us count parameters. For each head, we have three weight matrices of dimensionality (D, dhead), giving us in total

3 x D x dhead x nheads

parameters. If the head dimension times the number of heads is equal to the model dimension, this implies that the number of parameters is in fact 3 x D x D and therefore the same as if we head a single attention head with dimension D. Thus, we can organize all weights into a single matrix of dimension (D, D), and this is what PyTorch does, which makes the calculation much more efficient (and is also better prepared to process batched input, which our simplified code is not able to do).

It is instructive to take a look at the implementation of multi-head attention in PyTorch to see what happens under the hood. Essentially, PyTorch reshuffles the weights a bit to treat the head as an additional batch dimension. If you want to learn more, you might want to take a look at this notebook in which I go through the code and also demonstrate how we can recover the weights of the individual heads from the parameters in a PyTorch attention layer.

If you actually do this, you might stumble upon an additional feature that we have ignored so far – the attention mask. Essentially, the attention mask allows you to forbid the model to look at certain parts of the input when processing other parts of the input. To see why this is needed, let us assume that we want to use attention in the input of a decoder. When we train the decoder with the usual teacher forcing method, we provide the full sentence in the target language to the model. However, we of course need to prevent the model from simply peaking ahead by looking at the next word, which is the target label for the currently processed word, otherwise training is trivially successful but the network has not learned anything useful.

In an RNN, this is prevented by the architecture of the network, as in each time step, we only use the hidden state assembled from the previous time steps, plus the current input, so that network does not even have access to future parts of the sentence. In an attention-based model, however, the entire input is usually processed in parallel, so that the model could actually look at later words in the sentence. To solve this, we need to mask all words starting at position i + 1 when building the attention vector for word i, so that the model can only attend to words at positions less than or equal to i.

Technically, this is done by providing an additional matrix of dimension (L, L) as input to the self attention mechanism, called the attention mask. Let us denote this matrix by M. When the attention weights are computed, PyTorch does then not simply take the matrix product

Q \cdot K^T

but does in fact add the matrix M before applying the softmax, i.e. the softmax is applied to (a scaled version of)

Q \cdot K^T + M

To prevent the model from attending to future words, we can now use a matrix M which is zero on the diagonal and below, but minus infinity above the diagonal, i.e. for the case L = 4:

M = \begin{pmatrix} 0 & -\infty & -\infty & -\infty \\ 0 & 0 & -\infty & -\infty \\ 0 & 0 & 0 & -\infty \\ 0 & 0 & 0 & 0 \end{pmatrix}

As minus infinity plus any other floating point number is again minus infinity and the exponential in the softmax turns minus infinity into zero, this implies that the final weight matrix after applying the softmax is zero above the diagonal. This is exactly what we want, as it implies that the attention weights have the property

\alpha_{ij} = 0 \, \textrm{for } i < j

In other words, the attention vector for a word at position i is only assembled from this word itself and those to the left of it in the sentence. This type of attention mask is often called a causal attention mask and, in PyTorch, can easily be generated with the following code.

mask = torch.ones(L, L)
mask = torch.tril(mask*(-1)*float('inf'), diagonal = -1)
mask = mask.t()
print(mask)

This closes our post for today. We now understand attention, which is one of the major ingredients to a transformer model. In the next post, we will look at transformer blocks and explain how they are combined into encoder-decoder architectures.

Mastering large language models – Part VIII: encoder-decoder architectures and attention

The examples for LSTMs and RNNs that we have studied so far have one feature in common – the input and the output have the same length. We have seen that this is a natural choice for tasks like creating sentences based on a given prompt or attaching labels to each word in a sentence. There are, however, tasks for which this simple architecture cannot be used as we need to create a sentence based on an input of different length. To address this class of problems, encoder-decoder architectures have been developed which we will discuss today.

A good example to illustrate the challenge is machine translation. Here, we are given a source sequence, i.e. a sequence of token (x1, …, xS), maybe already vectorized, as input. The objective is to create a target sequence (y1, …, yT) as output representing the translation of the source sentence into a target language. Typically, the length T of the target sequence differs from the length S of the source sequence, which a single LSTM cannot easily cover.

Put differently, the objective is now no longer to model conditional probabilities for the completion of a sentence, i.e. probabilities of the form

P(w | w_1, \dots, w_n)

but conditional probabilities for a target sequence given the source sequence, i.e. the probability distribution

P(y_1, \dots, y_T | x_1, \dots, x_S)

The idea behind encoder-decoder architectures is to split this task into two subtasks, each of which is taken over by a dedicated network. First, there is a network called the encoder, that translates the source sequence into a single vector (or a concatentation of multiple vectors) called the context. The idea is that this vector represents, in a form independent of the length of the source sequence, an internal representation of the source sequence that somehow captures its meaning. Then a second network, the decoder, takes over. This network has access to the context and, given the context, creates the target sequence, as indicated in the diagram below..

In this general form, the idea is not bound to a specific type of network. Often, encoder and decoder are both LSTMs, but we will see in a later post that also transformer networks can be used in this way.

Let us now be a bit more specific on how we can bring this idea to live with LSTMs serving as decoders and encoders and specifically how these models are trained. For the encoder, this is easy – as we want the model to compress the meaning of the source sentence in the context, we of course need to feed the source sentence into the encoder. For the decoder, it is common to again apply teacher forcing. However, to create the first word of the target sentence, we need a starting point for the model. Therefore, the encoded sentences typically contain a “beginning of sentence” token, and it is also common practice to conclude the source sentence with a “end of sentence token”.

During inference, the model receives the source sequence as input and the first item of the target sequence, i.e. the beginning-of-sentence token. We can then apply any of the sampling methods discussed in an earlier post to successively generate the next word, until the model emits an end-of-sentence marker and the translation is complete.

Unfortunately, there is a fundamental problem with this architecture. If you look at the diagram, you will see that the context is the only connection between the encoder and the decoder. Consequently, the network has to compress all information necessary for the generation of the target sequence into the context, which is typically a vector of fixed size. Especially for longer source sentences, this quickly creates a bottleneck.

In 2015, Bahdanau, Cho and Bengio proposed a mechanism called attention to solve this issue. In their paper, they describe an approach which, instead of using a fixed-length context vector shared by all time steps of the decoder, uses a time-dependent context vector.

Specifically, each time step of the decoder receives three different inputs: the decoder input xt (which, as in the diagram above, is the previous word of the target sentence), the previous hidden state ht-1 and, in addition, a step-specific context ct. This context is assembled from the outputs os of the encoder network (these are in fact not exactly the hidden states, as the architecture proposed here uses a so-called bidirectional RNN as encoder, but let us ignore this for the time being). More precisely, each context vector ct is a weighted linear combination

c_t = \sum_s \alpha_{ts} o_s

of all outputs of the encoder network at all time steps. Thus, each decoder step has access to the full output of the encoder. However, and this is the crucial point, the way how the weights are calculated is governed by learned parameters which the network can adapt during training. This allows the decoder to focus on specific parts of the input sequence, depending on the current time step, i.e. to put more attention on specific time steps, lending the mechanism its name. Or, as the original paper puts it nicely in section 3.1:

“The decoder decides parts of the source sentence to pay attention to. By letting the decoder have an attention mechanism, we relieve the encoder from the burden of having to encode all information in the source sentence into a fixed length vector.“

To illustrate this, the authors include some examples for the weights used by the network. Let us look at the first of them, which illustrates the weights while translating the english sentence “The agreement on the European Economic Area was signed in 1992.”

We see that, as envisioned, the network learns to focus on the word that is currently being translated, even though the order of words in target and source sentence are different.

Attention turned out to be a very powerful idea. In fact, attention is so useful that it gave rise to a new class of language models which works without the need to have a hidden state which is updated sequentially over time. This new generation of networks is called transformers, and we will start to look at transformers and at attention scores in more detail in the next post.

References:

[1] Sequence to Sequence learning with Neural Networks, Sutskever et al.
[2] Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation, Cho et al.
[3] Speech and Language Processing by Jurafsky and Martin, specifically chapter 9
[4] Neural Machine Translation and Sequence-to-sequence Models by Neubig
[5] Neural Machine Translation by Jointly Learning to Align and Translate, D. Bahdanau, K.Cho, Y. Bengio

Mastering large language models – Part VII: War and Peace

This blog is all about code – we will implement and train an LSTM on Tolstoys War and Peace and use it to generate new text snippets that (well, at least very remotely) resemble pieces from the original novel. All the code can be found here in my GitHub repository for this series.

First, let us talk about the data we are going to use. Fortunately, the original novel is freely available in a text-only format at Project Gutenberg. The text file in UTF-8 encoding contains roughly 3.3 million characters.

After downloading the book, we need to preprocess the data. The respective code is straightforward – we tokenize the text, build a vocabulary from the list of token and save the vocabulary on disk. We then encode the entire text and save 90% of the data in a training data set and 10% of the data in a validation data set.

The tokenizer requires some thoughts. We cannot simply use the standard english tokenizer that comes with PyTorch, as we want to split the text down to the level of the individual characters. In addition, we want to compress a sequence of multiple spaces into one, remove some special characters and replace line breaks by spaces. Finally, we convert the text into a list of characters. Here is the code for a simple tokenizer that does all this.

def tokenize(text):
    text = re.sub(r"[^A-Za-z0-9 \-\.;,\n\?!]", '', text)
    text = re.sub("\n+", " ", text)
    text = re.sub(" +", " ", text)
    return [_t for _t in text]

The preprocessing step creates three files that we will need later – train.json which contains the encoded training data in JSON format, val.json which contains the part of the text held back for validation and vocab.pt which is the vocabulary.

The next step is to assemble a dataset that loads the encoded book (either the training part or the validation part) from disk and returns the samples required for training. Teacher forcing is implemented in the __getitem__ method of the dataset by setting the targets to be the input shifted by one character to the right.

def __getitem__(self, i):
    if (i < self._len):
        x = self._encoded_book[i: i + self._window_size]
        y = self._encoded_book[i + 1: i + self._window_size + 1]
        return torch.tensor(x), torch.tensor(y)
    else:
        raise KeyError

For testing, it is useful to have an implementation of the dataset that uses only a small part of the data. This is implemented by an additional parameter limit that, if set, restricts the length of the dataset artificially to a given number of token.

Next let us take a look at our model. Nothing here should come as a surprise. We first use an embedding layer to convert the input (a sequence of indices) into a tensor. The actual network consists of an LSTM with four layers and an output layer which converts the data back from the hidden dimension to the vocabulary, as we have used it before. Here is the forward method of the model which again optionally accepts a previously computed hidden layer – the full model can be found here.

def forward(self, x, hidden = None):
    x = self._embedding(x) # shape is now (L, B, E)
    x, hidden = self._lstm(x, hidden) # shape (L, B, H)
    x = self._out(x)
    return x, hidden

Finally, we need a training loop. Training proceeds as in the examples we have seen before. After each epoch, we perform a validation run, record the validation loss and save a model checkpoint. Note, however, that training will take some time, even on a GPU – be prepared for up to an hour on an older GPU. In case you want to skip training, I have included a pretrained model checkpoint in the GitHub repository, so if you want to run the training yourself, remove this first. Assuming that you have set up your environment as described in the README, training therefore proceeds as follows.

cd warandpeace
python3 preprocess.py
# Remove existing model unless you want to pick up from previous model
rm -f model.pt
python3 train.py

Note that the training will look for an existing model model.pt on disk, so you can continue to train using a previously saved checkpoint. If you start the training from scratch and use the default parameters, you will have a validation loss of roughly 1.27 and a training loss of roughly 1.20 at the end of the last epoch. The training losses are saved into a file called losses.dat that you can display using GNUPlot if that is installed on your machine.

In case you want to reproduce the training but do not have access to a GPU, you can use this notebook in which I have put together the entire code for this post and run it in Google Colab, using one of the freely available GPUs. Training time will of course depend on the GPU that Google will assign to your runtime, for me training took roughly 30 minutes.

After training has completed (or in case you want to dive right away into inference using the pretrained model), we can now start to sample from the model. 

python3 predict.py

The script has some parameters that you can use to select a sampling method (greedy search, temperature sampling, top-k sampling or top-p sampling), the parameters (temperature, k, p), the length of the sample and the prompt. Invoke the script with

python3 predict.py --help

to get a summary of the available parameters. Here are a few examples created with the standard settings and a length of 500 characters, using the model checked into the repository. Note that sampling is actually fast, even on a CPU, so you can try this also in case you are not working on a CUDA-enabled machine.

She went away and down the state of a sense of self-sacrifice. The officers who rode away and that the soldiers had been the front of the position of the room, and a smile he had been free to see the same time, as if they were struck with him. The ladies galloped over the shoulders and in a bare house. I should be passed about so that the old count struck him before. Having remembered that it was so down in his bridge and in the enemys expression of the footman and promised to reach the old…

Thats a wish to be a continued to be so since the princess in the middle of such thoughts of which it was all would be better. Seeing the beloved the contrary, and do not about that a soul of the water. The princess wished to start for his mother. He was the princess and the old colonel, but after she had been sent for him when they are not being felt at the ground of her face and little brilliant strength. The village of Napoleon was stronger difficult as he came to him and asked the account

Of course this is not even close to Tolstoy, but our model has learned quite a bit. It has learned to assemble characters into words, in fact all the words in the samples are valid english words. It has also learned that at the start of a sentence, words start with a capital letter. We even see some patterns that resemble grammar, like “Having remembered that” or “He was the princess”, which of course does not make too much sense, but is a combination of a pronoun, a verb and an object. Obviously our model is small and our training data set only consists of a few million token, but we start to see that this approach might take us somewhere. I encourage you to play with additional training runs or changed parameters like the number of layers or the model dimension to see how this affects the quality of the output.

In the next post, we will continue our journey through the history of language models and look at encoder-decoder architectures and the rise of attention mechanisms.