Superconducting qubits – on islands, charge qubits and the transmon

In my previous post on superconducting qubits, we have seen how a flux qubit represents a qubits state as a superposition of currents in a superconducting loop. Even though flux qubits have been implemented and used successfully, most research groups today focus on different types of qubits using a charge qubit as an archetype.

Charge qubits – the basics

The basic idea of a superconducting charge qubit is to create a small superconducting area called the island which is connected to a circuit in such a way that we can control the number of charge carries that are located on the island. A typical way to do this is shown in the diagram below.

In this diagram, we see, in the upper left, a Josephson junction, indicated by the small cross. Recall that a Josephson junction consists of two superconducting electrodes separated by a thin insulator. Thus a Josephson junction has a capacity, which is indicated by the capacitor C in the diagram.

On the right of the Josephson junction is a second capacitor. Now charge carriers, i.e. Cooper pairs, can tunnel through the Josephson junction and reach the area between the second capacitor and the junction – this is our island. Conversely, Cooper pairs can cross the junction to leave the island again. The flow of Cooper pairs into the island and away from the island can be controlled by applying an external voltage V_g. Effectively, a certain number of Cooper pairs will be trapped on the island – this is why this circuit is sometimes called a Cooper pair box – but this number will be subject to quantum fluctuations due to tunneling through the junction. Roughly speaking, these fluctuations cause an oscillation which will give us energy levels, and we can use two of these energy levels to represent our qubit.

Let us try to understand how these energy levels look like. Again, I will try to keep things short and refer to my more detailed notes on GitHub for more details. The Hamiltonian for our system looks as follows.

Here, E_g and E₀ are energies that are determined by the geometry of the junction and the value of the capacities in the circuit, N is the number of Cooper pairs on the island, N_g is a number depending on the external voltage and is (proportional to) the flux through the junction. Thus N and are our dynamic variables, representing the number of Cooper pairs on the island and its change over time, whereas the other quantities are parameters determined by the circuit and the external voltage. As N_g depends on the external voltage and can therefore be changed easily, this is the parameter we will be using to tweak our qubit.

Using a computer algebra program (or this Python notebook), it is not difficult to obtain a numerical approximation of the eigenvalues of this operator (we can, for instance, represent the Hamiltonian as a matrix subject to an eigenbasis for N and calculate its eigenvalues after cutting off at a finite dimension). The diagram below shows the results for E₀ = 0.1 E_c.

We see that if N_g is an integer, there is a degeneracy between the first and second excited state. If, however, N_g is a half-integer, then this degeneracy is removed, and the first two energy levels are fairly well separated from the rest of the spectrum.

With this relation of the two energies E_C and E₀, the probability for a Cooper pair to tunnel through the Josephson junction is comparatively small. Thus, the fluctuations in the quantum number N are small, and the eigenstates of N are almost stationary and therefore almost energy eigenstates. As the energy levels are well separated, we can use the first two energy levels as a qubit. As the eigenstates of the operator representing the charge on the island are almost stationary states, this regime is called the charge regime and the resulting qubit is called the charge qubit.

The transmon

This is all nice, but in practice, there is still a problem. To understand this, let us take a look at the energy level diagram above again. The energy levels are not flat, meaning that a change in the value of N_g is changing the energy levels and therefore the stationary states. Unfortunately, the value of N g does not only depend on the external voltage V_g (which we can control), but also on charge noise, i.e. unwanted charge fluctuations that are hard to suppress.

Therefore, the charge qubit is quite sensitive to charge noise. The point N_g = 0.5, called the sweet spot, is typically chosen because at this point, at least the first derivative of the energy as a function of the charge vanishes, so that the qubit is only affected by charge noise to the second order. However, this dependency remains and limits the coherence time of the charge qubit.

One way to reduce the sensitivity to charge noise is to increase the ratio between E₀ and E_C . To understand what happens if we do this, take a look at the following diagram which displays the first few energy levels when this ratio is 5.0

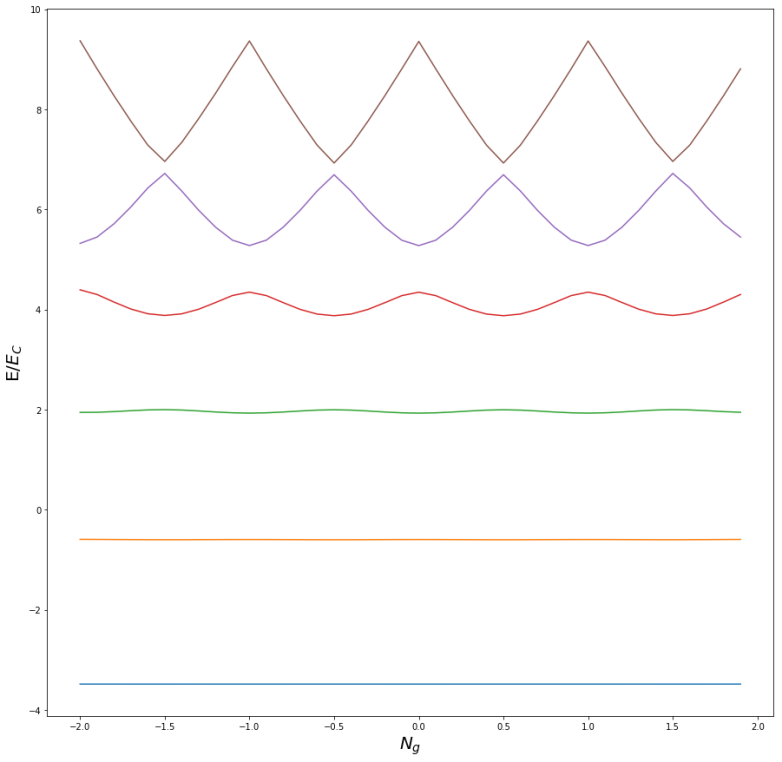
We see that, compared to our first energy level diagram, the sensitivity to charge noise is reduced, as the energy of the first two energy levels is almost flat, with a minimal dependency on N_g . However, this comes at the cost of a more equidistant spacing of the energy levels, making the isolation between the first two energy levels and the rest of the spectrum hard, and the question arises whether we gain an advantage at the cost of another one.

Fortunately, it turns out that the sensitivity to charge noise decreases exponentially fast, but the anharmonicity of the energy levels decreases much slower. Thus there is a region for the ratio E₀ / E_c in which this sensitivity is already comparatively low, but the energy levels are still sufficiently anharmonic to obtain a reasonable two-level system. A charge qubit operated in this regime is called a transmon qubit.

Technically, a larger value of E₀ compared to E_C is achieved by adding an additional capacitor parallel to the Josephson junction. If we use a high value for the additional capacity, we can make E_C arbitrarily small and can achieve an arbitrary high ratio of E₀ compared to E_C.

To develop a physical intuition of why this happens, recall that the energy E₀ of the Josephson junction measures the tunneling probability. If E₀ is large compared to E_C , it is comparatively easy for a Cooper pair to tunnel through the junction. Therefore the phase difference across the junction will only fluctuate slightly around a stationary value, i.e. the wave function will be localized sharply in the -space. Consequently, the charge N will no longer be a good quantum number and the charge eigenstates will no longer be approximate energy eigenstates. Instead, we will see significant quantum fluctuations in the charge, which makes the system more robust to external charge noise. In this configuration, you should therefore think of the qubit state not as a fixed number of Cooper pairs on the island, but more as a constant tunneling current flowing through the junction.

To control and read out a transmon qubit, it is common to use a parallel LC circuit which is coupled with the transmon via an additional capacitor. Using microwave pulses to create currents in that LC circuit, we can manipulate and measure the state of the qubit and couple different qubits. Physically, the LC circuit is realized as a transmission line resonator, in which – similar to an organ pipe – waves are reflected at both ends and create standing wave patterns (that transmission lines are used is the reason for the name transmon qubit).

At the time of writing, most major players (Google, IBM, Rigetti) are experimenting with transmon based qubit designs, as it appears that this type of qubit is most likely to be realizable at scale. In fact, Transmon qubits are the basic building blocks of Google’s Bristlecone architecture as well as for IBMs Q experience and Rigettis QPU.

To learn more, I recommend this and this review paper, both of which are freely available on the arXiv.