In some of the last posts in my series on quantum computing, we have discussed how NMR (nuclear magnetic resonance) technology can be used to implement quantum computers. Over the last couple of years, however, a different technology has attracted significantly more interest and invest – superconducting qubits.
What are superconducting qubits? To start with something a bit more familiar, let us look at an analogue in classical electronics – an LC circuit. If you have ever built a transistor-based radio, you will have seen this. An LC circuit consists of an inductor and a capacitor, connected together as follows.
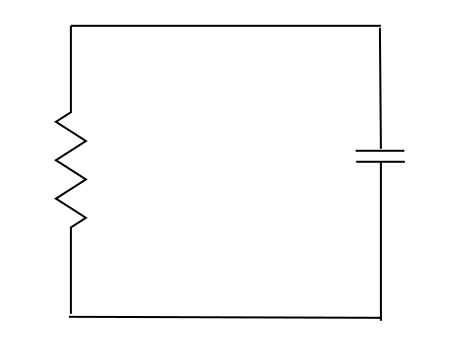
To understand what this circuit is doing, let us assume that at some point in time, the capacitor is fully charged. Then current will start to flow through the inductor. This will create a magnetic field in the inductor, so the electric energy stored in the capacitor is transformed into magnetic energy stored in the magnetic field of the inductor. Once the capacitor is fully decharged, the magnetic field will start to break down, again inducing a current which will then recharge the capacitor and so forth. This follows a pattern that every physicist knows by the name harmonic oscillator.
Now, in quantum mechanics, a harmonic oscillator has an infinite number of energy levels at equally spaced values. Can we use two of them, say the ground state and the first excited state, to build a qubit? Unfortunately there are a few obstacles.
The first problems is that an ordinary current is the coordinated movement of many electrons that constantly interact with the environment (dissipating heat due to the non-zero resistance) and therefore do not make a good closed quantum system. Even though each individual electron is of course a quantum mechanical system, the overall system exhibits classical behavior.
This changes if we use a superconducting LC circuit. As soon as we enter the superconducting regime, the flow of charge is no longer given by individual moving electrons, but by Cooper pairs that flow through the conductor. It is well known that in this state, the system can be described by a macroscopic wave function and is therefore behaving according to the laws of quantum mechanics, leading to phenomena like the quantization of the magnetic flux in a superconducting loop.
Does this mean that we can use a superconducting LC circuit, which then should behave as a quantum mechanical harmonic oscillator, as a qubit? Well, we are not quite there yet – as the energy levels of a harmonic oscillator are equally spaced, the first two levels are not well isolated against the remaining levels which makes it very hard to confine the system to these two levels.
Enter Josephson junctions. A Josephson junction is a superconducting element which consists of two superconducting solids that are separated by a thin insulator, like displayed schematically below.
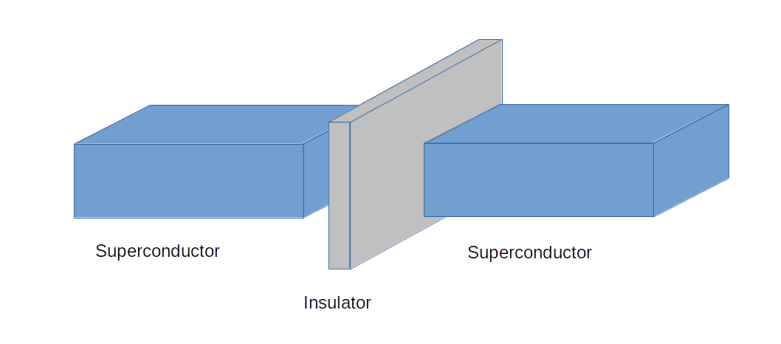
Due to tunneling, Cooper pairs can cross the junction and thus a superconducting current can flow through the element. It turns out that a Josephson junction behaves like an inductor whose inductance is not constant (as for an ordinary inductor), but depends on the current. This will change the Hamiltonian of the system to the effect that the energy levels become distorted. If we get the parameters right, we are able to obtain a situation where the two lowest energy levels are separated fairly well from the rest of the energy spectrum and therefore the corresponding subsystem can approximately be treated as a two-level system, i.e. a qubit.
Superconducting qubits have gained a lot of attention over the last two years. They can be produced with techniques known from the production of integrated circuit, and they can be controlled with classical electronics. Their dimensions are within the realm of traditional IC technology, being in the micrometer range. The picture below (credits A. ter Haar, PhD thesis) shows a superconducting qubit (a so-called flux qubit) made of an inner loop with three Josephson junctions and an outer loop for readout and control.

In addition, superconducting qubits can easily be layed out on a chip, which makes them good candidates for small, highly integrated quantum computing devices. Of course they need cooling as the need to operate below the critical temperature of the employed superconducting material, but this is standard technology by now. Today, most of the big players in the quantum world like Google, IBM, Rigetti and D-Wave are focusing their efforts on superconducting qubits.
To interact with the qubit (and to make two qubits interact), there are several options. We can apply an external voltage, an external current or couple the system with a microwave cavity acting as a resonator. We also have several choices to combine a Josephson junction with classical circuits – we can add an additional capacitor in series with the Josephson junction (which will give us a qubit called the charge qubit), combine this setup with an additional capacitor parallel to the Junction (transmon qubit) or use a Josephson junction in combination with a classical inductance formed by a superconducting loop (flux qubit). All these circuits have different characteristics and have been used to realize qubits. The flux qubit, for instance, is being used in the D-Wave quantum annealer, whereas Google uses transmon qubits for their devices. We will dive a little bit deeper into each of them in the next posts in this series.
